17. Feuille 1 : fonctions

Rappels

• Le symbole \(\blacksquare\) indique les exercices ou questions obligatoires. Commencez par ceux-là.

• Les symboles \(\star\) et \(\star\star\) indiquent les exercices ou questions de difficulté relative plus importante.

Notations

• Les identifiants des fonctions à écrire sont donnés avec des parenthèses vides : factorielle(), moy(), … Non pas parce que ces fonctions sont sans argument/paramètre. Mais juste pour fixer l’identifiant et vous laisser définir les paramètres nécessaires au traitement.

Focus

• Fonctions

Compétences

• utiliser une fonction prédéfinie ou existante

• définir et écrire la spécification d’une fonction qui réalise un traitement décrit en français, ou qui résout un problème (simple) décrit en français

• définir et écrire des appels simples (ou des tests unitaires)

• définir, écrire et utiliser des tests unitaires

• définir et écrire l’implémentation d’une fonction associée à une spécification

Rappel de quelques consignes

Dans cet ordre et avec les corrections entre 2 étapes si besoin :

1. écriture de la signature de la fonction docstring compris

2. écriture d’au moins un appel simple ou un test unitaire

3. écriture du corps

4. écriture des tests unitaires

5. exécution des tests unitaires

6. écriture des appels voulus

7. exécution des appels voulus

Se souvenir :

• Séparer les entrées-sorties des traitements !

• Réduire au minimum l’utilisation des input() (les entrées au clavier) et des print() (les sorties à l’écran).

• Utiliser des identifiants différents pour les paramètres formels et effectifs, respectivement dans la définition et les appels.

17.1. Objectif 10

17.1.1. \(\blacksquare\) Exercice. (factorielle)

La valeur de factorielle (de) \(n\), où \(n\) est un entier positif, est : \(n ! = 1 \times 2 \times \cdots \ \times (n-1) \times n\). On choisit \(0 ! = 1\).

2. Écrire la fonction factorielle() qui calcule et retourne \(n!\).

3. La fonction factorial() du module math effectue le même calcul. Utiliser cette fonction pour définir et coder des tests unitaires de votre fonction factorielle().

4. Utiliser la fonction factorielle() pour écrire des fonctions qui calculent les quantités suivantes.

   1. Le nombre d’arrangements (listes ordonnées) de \(k\) valeurs prises dans un ensemble de \(n\) valeurs est : \(\mathcal{A}_n^k = {n !}/{(n-k)!}, (k \le n)\).

   2. Le nombre de combinaisons (listes non ordonnées) de \(k\) valeurs prises dans un ensemble de \(n\) valeurs est : \(\left(_k^n\right) = {\mathcal{A}_n^k}/{k!}\), \((k \le n)\).

17.1.2. \(\blacksquare\) Exercice (nouvelle formulation)

1. Relire les consignes rappelées avant l’exercice précédent.

2. Lire l’exercice en entier avant de commencer.

3. Écrire une fonction moy() qui calcule et retourne la moyenne de 4 valeurs flottantes.

4. Écrire quelques tests unitaires bien choisis.

5. Utiliser la fonction moy() pour réaliser le traitement suivant.

   • Ces quatre valeurs sont entrées au clavier et stockées dans un tableau.

   • La moyenne calculée est affichée à l’écran avec un rappel des quatre valeurs correspondantes.

17.1.3. \(\blacksquare\) Exercice

On rappelle quelques suites et séries numériques classiques.

• La somme des \(n\) premiers entiers : \(s_1(n) = 1 + 2 + \cdots + (n-1) + n = \sum_{k=1}^{n} k\) ;

• La suite de Fibonacci : \(u_{n+1} = u_{n}+ u_{n-1}\) et \(u_0=u_1=1\).

• Une suite arithmético-géométrique : \(u_{n+1} = u_n/3 + 2\) avec \(u_0=1\).

1. Écrire des fonctions qui calculent et retournent le \(n\)-ième terme de ces suites.

2. Écrire des tests unitaires adaptés. Justifier vos choix.

3. Pour chacune de ces suites et en utilisant ces fonctions, lire une valeur de \(n\) entrée au clavier, calcule le \(n\)-ième terme de la suite puis l’afficher à l’écran.

17.1.4. Exercice

1. \(\blacksquare\) Définir et écrire une fonction est_rectangle() qui vérifie si un triangle est rectangle. Aucune hypothèse est effectuée sur les paramètres de ce traitement.

2. Ecrire des tests unitaires adaptés. Justifier vos choix.

17.1.5. Exercice (codage ASCII)

L’ASCII est un codage de caractères qui définit 128 codes sur 7 bits. Chaque code correspond à un caractère : chiffres, lettres, symboles mathématiques et de ponctuation.

En Python, la fonction ord() retourne le code ASCII d’un caractère fourni en argument. La fonction chr() retourne le caractère associé à un code donné.

1. Ecrire un programme qui affiche les 128 codes ASCII selon 16 lignes de 8 colonnes.

Remarque. Etre conscient que cette question nécessite de mélanger des traitements (appels de fonctions) et des entrées-sorties (print()).

2. Ecrire une autre solution qui ne mélange pas traitements et entrées-sorties.

17.1.6. \(\blacksquare\) Exercice (tableaux 1D)

1. Écrire une fonction tabup() qui vérifie si les n valeurs d’un tableau sont rangées par ordre croissant. Ces valeurs sont des entiers.

2. Accompagner votre développement avec quelques tests unitaires bien choisis.

3. Proposer des solutions itératives alternatives (for vs. while) lorsque qu’elles conduisent à des traitements différents.

17.1.7. \(\blacksquare\) Exercice

Soit t un tableau 1D d’entiers de taille n arbitraire. Voici quelques traitements classiques de ces tableaux et les fonctions associées.

1. max_tab() qui calcule et retourne la valeur maximale d’un tableau 1D.

2. max_ind_max() qui calcule et retourne le plus grand indice de la valeur maximale d’un tableau 1D.

3. min_ind_max() : une modification de la fonction précédente qui calcule et retourne le plus petit indice de la valeur maximale d’un tableau 1D.

4. Tests unitaires : pour chacune de ces fonctions, expliciter différents tableaux t qui correspondent, le cas échéant, à des cas particuliers de traitement. Les tester pour valider vos solutions.

17.1.8. \(\blacksquare\) Exercice (extrait d’examen 2017 sans machine)

1. Que calcule la fonction m suivante ?

    def m(s : str, n : int, c : str ) -> int: 
        ''' role : à vous de deviner :) '''
        res = 0
        for i in range(n): 
            if s[i] == c: 
                res = res + 1 
        return res

2. Quel résultat produit l’exécution du code suivant ?

    t = "anticonstitutionnellement" 
    nba = m(t, len(t), 'a') 
    nbe = m(t, len(t), 'e') 
    nbl = m(t, len(t), 'l') 
    print(len(t), nba, nbe, nbl)

3. Utiliser la fonction m pour écrire une fonction mm qui identifie et retourne la lettre ayant le maximum d’occurrences dans une chaîne de caractères de longueur n. Si plusieurs lettres conviennent, l’algorithme identifiera celle dont l’occurrence est la plus tardive dans s. Par exemple 'o' dans 'toto'.

Accompagner cette fonction de quelques tests unitaires pertinents.

4. Écrire le code qui utilise mm et fournit l’affichage suivant.

t est la lettre qui apparaît le plus ( 5 fois) dans anticonstitutionnellement
o est la lettre qui apparaît le plus ( 2 fois) dans toto

5. Modifier mm pour que dans le cas d’une occurrence maximale multiple, l’algorithme identifie la lettre de première occurrence. Par exemple, 't' dans 'toto'.

6. Réécrire la fonction mm de cette question sans utiliser la fonction m. Vérifier que les tests unitaires écrits plus haut valident cette version.

(exo:palindromeiter)

17.1.9. \(\blacksquare\) Exercice (palindrome)

Un palindrome est un mot, ou un groupe de mots, dont l’ordre des lettres reste le même qu’on le lise de la droite vers la gauche ou inversement. Des exemples bien connus sont “été”, “kayak”, “mon nom”, “élu par cette crapule”. Ce dernier permet d’illustrer qu’on ne tient pas compte en général des accents, trémas, cédilles, ni des espaces. Dans cet exercice :

• un mot ou un groupe de mots est représenté par une chaîne de caractères (str),

• ces caractères sont sans accent, tréma, ni cédille : “ete”

• les espaces sont considérés comme des caractères : ainsi “elu par cette crapule” n’est pas un palindrome ici.

1. Ecrire une fonction qui teste si un argument est ou non un palindrome et retourne le booléen correspondant.

2. Valider votre fonction avec des tests unitaires.

17.1.10. Exercice (produit scalaire)

Rappel : le produit scalaire deux vecteurs orthogonaux est nul.

Ecrire les fonctions qui vérifie l’orthogonalité ou non de vecteurs

1. de taille 3,

2. de taille arbitraire \(n\).

17.1.11. \(\blacksquare\) Exercice (tableau 2D)

1. Écrire une fonction qui, pour les deux paramètres entiers a et b (\(a \le b\)), calcule la table de multiplication entre les entiers compris entre a et b inclus. Le résultat attendu est un tableau 2D, de dimension adaptée, qui est aussi un paramètre d’entrée de cette fonction. Après traitement, la case \((i,j)\) de ce tableau contient le résultat de \(i \times j\). La table des multiplications entre 1 et 10 est obtenue pour \(a = 1\) et \(b= 10\).

2. Utiliser cette fonction pour afficher cette table pour des valeurs de a et b entrées au clavier.

17.1.12. \(\blacksquare\) Exercice (matrices)

Ecrire les algorithmes de vérification suivants pour une matrice \(M\) donnée, carrée de taille \(n\) et à valeurs flottantes.

1. \(M\) est diagonale ?

2. \(M\) est symétrique ?

3. \(M\) est égale à l’identité ?

4. \(M\) est l’inverse d’une autre matrice donnée \(N\) ?

17.2. Objectif 20

Consignes importantes

1. Proposer les fonctions les plus générales possibles.

2. Accompagner chaque fonction écrite de quelques tests unitaires pertinents.

17.2.1. Exercice (math)

On continue l’exercice.

• Utiliser la fonction factorielle() pour écrire des fonctions qui calculent les quantités suivantes.

• En s’inspirant d’un exemple donné au chapitre 1, proposer des représentations graphiques qui illustrent les approximations mentionnées. Le chapitre Modules utiles du support du cours présente le module matplotlib.pyplot utile à ce traitement.

1. Une approximation de \(e \approx \sum_{k=0}^n 1/k !\), puis vérifier que l’approximation est d’autant plus précise que \(n\) est grand.

2. La formule de Stirling \(n! \approx \sqrt{2\pi n} (n/e)^n\) qui donne un équivalent de la factorielle (et aussi une approximation de \(\pi\)), approximation dont on vérifiera la pertinence.

3. Même question pour \(\ln(n!) \approx n\ln(n)-n\) et des \(n\) assez grands.

17.2.2. Exercice (crible d’Eratosthène)

1. Consulter la page wikipedia du crible d’Eratosthène

2. Écrire une fonction est_premier() qui retourne un booléen qui indique si un nombre entier donné \(n\) est premier ou non.

(exo:pgcd)

17.2.3. Exercice (pgcd)

Écrire une fonction pgcd() qui calcule le PGCD de deux entiers naturels. On utilisera l’algorithme d’Euclide.

Rappel : l’algorithme d’Euclide utilise la propriété suivante. Le PGCD de \(a\) et \(b\), \(a > b\), est égal à \(b\) si le reste \(r\) de la division euclidienne de \(a\) par \(b\) est nul, sinon il vaut le PGCD de \(b\) et de \(r\). Le PGCD de 2 nombres distincts premiers entre eux (i.e. sans diviseur commun autre que 1) est égal à 1. Cet exercice permet d’écrire une version itérative de cet algorithme.

17.2.4. Exercice (tableau 1D, écriture décimale)

Ecrire une fonction qui transforme un tableau de 0 et de 1 de longueur arbitraire, en l’entier de base 10 qui est codé par ce tableau en représentation de position en base 2 :

\[ (b_n b_{n-1} \cdots b_1 b_0)_2 = (\sum_{i=0}^n b_i \times 2^i)_{10} \text{ avec } b_i \in \{0, 1\}. \]

Exemple. la tableau \((1,0,1,1)\) représente l’entier \(8+0+2+1 = 11\).

17.2.5. (\(\star\)) Exercice (Algorithme de type Monte-Carlo)

On va calculer une approximation de \(\pi\) de façon probabiliste.

1. Ecrire une fonction qui vérifie si un point du plan défini par ses coordonnées \((x,y)\) appartient à un disque de centre \((a,b)\) et de rayon \(r\).
   Rappel. L’équation du cercle de mêmes caractéristiques est : \((x-a)^2 + (y-b)^2 = r^2\).

2. Identifier dans le chapitre Modules utiles du support de cours (ou la documentation du module python random), la fonction adaptée à la génération d’un point aléatoire dans le carré \([-1, 1] \times [-1, 1]\).

3. Soit \(\mathcal{C}\) le cercle de centre 0 et de rayon 1. Ecrire une programme qui génère \(n\) points aléatoires situés dans le carré précédent et calcule le ratio entre les points situés dans le cercle \(\mathcal{C}\) et \(n\).

4. Faire varier \(n\) et observer l’évolution de ce ratio.

5. (\(\star\)) En déduire une approximation de \(\pi\).

17.2.6. (\(\star\star\)) Exercice

On souhaite évaluer la valeur d’un polynôme de degré \(3\), \(p_3(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3\), en des valeurs \(x\) arbitraires.

1. Écrire une fonction eval() qui calcule et retourne \(p_3(x)\).

2. Ecrire un algorithme qui utilise cette fonction pour des valeurs entrées au clavier et affiche le résultat à l’écran.

3. (\(\star\)) Détailler le principe d’un algorithme qui calcule une racine d’un polynôme sur un intervalle \([a, b]\) donné. La présence d’une racine unique sur \([a, b]\) sera admise MAIS l’existence d’une racine sera vérifiée par cet algorithme. Introduire un paramètre adapté au caractère approximatif de la valeur calculée.

4. Écrire un algorithme principal qui effectue cette recherche pour un polynôme \(p_3\) de degré \(3\) et un intervalle \([a, b]\) donnés. Tous les paramètres sont entrés au clavier.

5. (\(\star\star\)) Appliquer cet algorithme pour retrouver, une à une, les racines de \(p(x)=x(x-1)(x-2)\). Ce polynôme sera considéré sous sa forme développée.

17.2.7. Exercice (tableau 2D)

Les fonctions suivantes seront définies et utilisées dans un programme (principal) qui définit des tableaux que vous choisirez pour vérifier la validité de vos traitements. Vous choisirez la structure de donnée la plus adaptée à ces traitements.

1. Ecrire une fonction est_egal() qui réalise la comparaison entre deux tableaux de dimension 1 et retourne le booléen correspondant. On convient que deux tableaux sont égaux si leurs tailles sont égales et si leurs valeurs sont égales deux à deux.

2. Ecrire une fonction nb_val_egales() qui retourne le nombre de valeurs égales deux à deux entre deux tableaux de dimension 1.

3. Pour chacune de ces fonctions, proposer des solutions itératives alternatives (for vs. while) lorsque qu’elles conduisent à des traitements différents.

4. Reprendre les questions précédentes pour des tableaux 2D. L’égalité entre tableaux multi-dimensionnels suppose l’égalité des dimensions, des tailles deux à deux dans chaque dimension, et des valeurs deux à deux pour toutes les valeurs du tableau. De même pour le décompte des valeurs égales deux à deux.

17.2.8. Exercice (images NB)

Note. Cet exercice est inspiré d’un extrait de sujet d’examen. Il comporte des questions Objectifs 10 et Objectif 20.

Une image 2D peut être représentée par un tableau 2D de pixels.
Une image “noir et blanc” de taille \(L \times C\) est ainsi représentée par un tableau de \(L\) lignes et \(C\) colonnes, de 0 (pixel blanc) ou de 1 (pixel noir).
Les images suivantes sont des exemples d’images 3 \(\times\) 4.

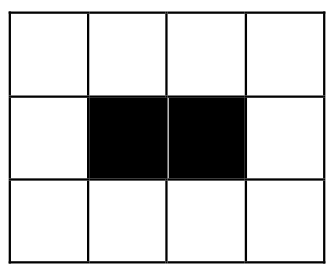
L’image blanche (à gauche) est représentée par le tableau de taille \(3 \times 4\) (une liste de listes de 0) donné par le code python suivant.

l = 3
c = 4
t = [[0 for i in range(c)] for j in range(l)]

print(t)
print(len(t), len(t[0]))

[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
3 4

Premières transformations d’images 3 \(\times\) 4.

1. Ecrire l’algorithme qui transforme l’image blanche (à gauche) en une image noire 3 \(\times\) 4 sans définir un autre tableau.

2. Ecrire l’algorithme qui transforme l’image blanche en l’image du centre.

3. Ecrire l’algorithme qui transforme l’image blanche en l’image de droite.

Fonctions et transformation d’image de taille arbitraire.

On considère la dernière transformation où la partie triangulaire inférieure est noircie. Selon la forme de la matrice, cette partie noircie est un triangle (matrice rectangulaire “allongée” horizontalement) ou un trapèze (matrice rectangulaire “allongée” verticalement). On va définir cette transformation sous la forme d’une fonction.

1. Ecrire l’en-tête de cette fonction tr()

2. Appliquer cette fonction à l’image blanche de gauche.

3. Ecrire le corps de la fonction tr().

4. (\(\star\)) Définir une image t2 de taille 4 \(\times\) 8 composée de lignes alternativement blanche et noire

5. On applique la fonction tr() à cette image. Dessiner “à la main” l’image ainsi transformée.

6. Ecrire ce traitement à l’aide de la fonction tr()

Analyse d’une image de taille arbitraire.

1. Ecrire une fonction nbpixblc() qui compte et retourne le nombre de pixels blanc d’une image de taille arbitraire

2. Que retourne l’application de cette fonction à l’image (4) de cette question.

17.2.9. Exercice.

De façon similaire à l’exercice précédent, on définit des images à niveaux de gris par un tableau 2D d’entiers compris en 0 (noir) et 255 (blanc). La taille de l’image \(largeur \times hauteur\) est arbitraire.
Ecrire les algorithmes des traitements suivants. On pourra commencer en introduisant un tableau supplémentaire pour l’image transformée. Selon les cas, on essaiera ensuite une solution “en place” : la transformation s’effectue sur le tableau de l’image d’origine.

1. Générer le négatif (reverse video) d’une image NB ou par niveaux de gris.

2. Générer une image NB à partir d’une image niveau de gris.

3. Augmenter le contraste de la transformation précédente.
   Principe : fixer un seuil et remplacer les pixels plus clairs que le seuil par des pixels blancs, et inversement les plus sombres que le seuil par des pixels noirs.

4. Générer une image miroir vertical (le haut se retrouve en bas et réciproquement) ou horizontal d’une image NB.

5. Augmenter la luminosité (ou luminance) d’une image à niveau de gris.
   Principe : ajouter ou retrancher une constante de la valeur des pixels.

6. Générer les contours significatifs d’une image.
   Principe : on remplace par un pixel noir chaque pixel dont la variation des valeurs de ses 4 voisins varient au delà d’un certain seuil, sinon on le remplace par un pixel blanc.

7. Réduire par 2 la taille d’une image à niveau de gris.
   Principe : chaque carré de 2x2 pixels est remplacé par 1 pixel de valeur la moyenne des pixels du carré.