Ctrl+K

Trier

6. Trier#

Mis à jour : May 15, 2025, lecture : 12 minutes minimum, PhL.

6.1. Introduction#

6.1.1. Vocabulaire#

Trier : classer, ordonner des valeurs, des objets

  • trier des copies par notes

  • trier des copies par ordre alphabétique des candidats

  • trier des livres dans une bibliothèque

  • trier des containers sur un port

Trier : To sort en anglais

  • Sorting algorithms

  • .sort() : méthode des list python

Pourquoi ?

  • recherche efficace : complexité linéaire \(\to\) complexité logarithmique si valeurs triées

  • applications multiples : binpack, correction orthographique, …

6.1.2. Complexités#

Tris en place

  • pas de duplication de l’ensemble à trier

  • complexité en espace constante vs. nombre de valeurs à trier

  • exemple : trier une main de cartes (tri par insertions)

Complexités en temps

  • algorithmes : tris (dits) lents \(\to\) tris (dits) rapides \(\to\) tris (dits) linéaires

  • complexité : quadratique \((n^2) \to\) semi-logarithmique (\((n\log(n)\)) \(\to\) linéaire \((n)\)

    • pires cas vs. meilleurs cas

  • la complexité optimale du tri par comparaisons est semi-logarithmique

Trier sans comparer des valeurs deux à deux !

  • Tris par comparaisons vs. tris par dénombrement

  • complexité en temps linéaire : très très efficaces

6.1.3. Principaux algorithmes de tri#

Tris par comparaisons : algorithmes lents

  • pire cas : quadratique

  • tri par sélections, par insertions, permutations, “à bulles”, …

Tris par comparaisons : algorithmes rapides

  • pire cas ou cas moyen : semi-log

  • tri fusion, tri (dit) rapide (quicksort)

Tris (dits) linéaires : applicabilité spécifique

  • exemple de restrictions : valeurs à trier = un ensemble fini d’entiers (ou une bijection vers un tel ensemble)

  • complexité en temps et en espace : linéaire

  • tri par dénombrements, tri par base (ou tri radix)

Rmq. pour la suite

Sans perte de généralités, les valeurs à trier sont supposées être \(n\) entiers stockés dans un tableau 1D (une liste python).

# si python<3.9
#from typing import List

6.2. Tri insertion#

Un exemple de tri par comparaisons, en place et de complexité au pire quadratique.

6.2.1. Principe#

Analogue au tri d’une main de cartes

  • je prends une carte pas encore correctement placée,

  • je parcours la partie triée de la main de cartes

  • et j’insère à sa bonne place la carte à classer

    • insérer une carte \(\Rightarrow\) en déplacer d’autres

6.2.2. (\(\star\)) Invariant#

(P) : Avant l’itération \(i\), le sous-tableau t[0, \(i\)[ est trié.

Exercice

  • Expliciter l’initialisation de (P).

  • Que signifie la terminaison de (P) ?

  • (\(\star\)) Prouver (P).

6.2.3. Algorithme#

def triInsertion(t : list[int], n: int) -> list[int]:
    '''tri insertion : version itérative
    entrées. t : tableau d entiers de longueur n = len(t)
    sortie. t est trié par ordre croissant'''
    for i in range(1, len(t)): # pour chaque valeur en partant de la gauche
        val = t[i]
        j = i
        while j > 0 and val < t[j-1]: # en remontant vers la gauche (partie triée)
            t[j] = t[j-1]
            j = j-1
        t[j] = val
    # le return n'est pas obligatoire : on a trié t en place (procédure)
    return t

# Premières applications

# un tableaux de valeurs aleatoires
from random import randint
dim = 5
a = [randint(0,50) for i in range(dim)]
print(a)
print("Trions !")
b = triInsertion(a, len(a))
print(b)
#print("attention : affecter un tab n'est pas creer un nouveau tab")
#print(a)

[26, 21, 25, 25, 19]
Trions !
[19, 21, 25, 25, 26]

6.2.4. Pire cas, meilleur cas#

Ces cas dépendent de l’ordre de parcours des valeurs à trier
- Nous avons choisi de parcourir ces valeurs par indices croissants : c-a-d. 1, 2, …, n-1

Pire cas : les valeurs sont dans un ordre inverse de l’ordre trié
- les valeurs sont décroissantes des indices 0 vers n-1

Meilleur cas : les valeurs sont déjà triées
- les valeurs sont croissantes des indices 0 vers n-1

# pire et meilleur cas
def pirecasinsertion(n: int) -> list[int]:
    a = [x for x in reversed(range(n))]
    return a

def meilleurcasinsertion(n: int) -> list[int]:
    a = [x for x in range(n)]
    return a


pire = pirecasinsertion(dim)
print("pire cas")
print(pire)
pire = triInsertion(pire, dim)
print(pire)
 
    
print("meilleur cas")
best = meilleurcasinsertion(dim)
print(best)
best = triInsertion(best, dim)
print(best)

pire cas
[4, 3, 2, 1, 0]
[0, 1, 2, 3, 4]
meilleur cas
[0, 1, 2, 3, 4]
[0, 1, 2, 3, 4]

Exercices#

  1. Expérimentation des pire et meilleurs cas du tri insertion
    a. Modifier triInsertion() pour décompter le nombre de comparaisons.
    b. Vérifier que les cas extrêmes exhibés sont bien ceux-là.
    C. Expérimenter en mesurant aussi les temps d’exécution.

  2. (*) Ecrire une version récursive de triInsertion()

Correction des exercices#

Sauter ce passage en première lecture

Hide code cell content 
from random import randint
from numpy import log
import matplotlib.pyplot as plt
from matplotlib.backends.backend_pdf import PdfPages
Hide code cell content 
valmax = 99

def triinsertion(t: list[int]) -> list[int]:
    '''Même version sans le paramètre n'''
    for i in range(1, len(t)):
        v = t[i]
        j = i
        while j > 0 and v < t[j-1]:
            t[j] = t[j-1]
            j = j-1
        t[j] = v
    return t


def comptriinsertion(t: list[int]) -> list[int]:
    """ version avec decompte du nb comparaisons"""
    c = 0 
    for i in range(1, len(t)):
        v = t[i]
        j = i
        c += 1 # au moins une (derniere) comparaison
        while j > 0 and v < t[j-1]:
            t[j] = t[j-1]
            j = j-1
            c += 1
        t[j] = v
        if j == 0:
            c = c-1 # sauf si c'est j qui arrete la boucle
    return t, c
Hide code cell content 
# un tableau de valeurs aléatoires
def tabalea(n : int) -> list[int]:
    a = [randint(0,valmax) for i in range(n)]
    return a

def pirecasinsertion(n: int) -> list[int]:
    a = [x for x in reversed(range(n))]
    return a

def meilleurcasinsertion(n: int) -> list[int]:
    a = [x for x in range(n)]
    return a
Hide code cell content 
def testcomp10():
    n = 10
    a = tabalea(n)
    w = pirecasinsertion(n)
    b = meilleurcasinsertion(n)
    tabs = [b,w,a]
    print("Trions !")
    for t in tabs:
        print(t)
        res, c = comptriinsertion(t)
        print(res)
        print(c , "comparaisons pour n = ", n)
Hide code cell content 
def testcomp():
    #dims = (10, 50)
    dims = (10, 50, 100, 200, 300, 500, 1000)
    nbcompalea = []*len(dims)
    nbcompbest = []*len(dims)
    nbcompworst = []*len(dims)
    for n in dims:
        b = meilleurcasinsertion(n)
        res, c = comptriinsertion(b)
        nbcompbest.append(c)
        print("Meilleur cas : au plus ", c , "comparaisons pour n = ", n)
        
        w = pirecasinsertion(n)
        res, c = comptriinsertion(w)
        nbcompworst.append(c)
        print("Pire cas : au moins ", c , "comparaisons pour n = ", n)
              
        p = 10
        print("Moyenne de ", p, "cas aleatoires :")
        ctot = 0
        for t in range(p):
            a = tabalea(n)
            res, c = comptriinsertion(a)
            #print(res)
            print(c , "comparaisons pour n = ", n)
            ctot += c
        cmoy = int(ctot/p)
        nbcompalea.append(cmoy)
        print("Conclusion : ", cmoy, "comparaisons en moyenne pour n = ", n, "(", p, "echantillons)")
        print("---------")
    return dims, nbcompbest, nbcompworst, nbcompalea


def plottestcomp():
    '''Pour tracer cette analyse. A effectuer hors notebook.'''
    # calculs
    n, b, w, m = testcomp()

    # traces
    fig = plt.figure()
    fig.suptitle("Complexites du tri insertion", fontweight='bold')
    
    # echelle lineaire
    #fig1 = fig.add_subplot(1,1,1)
    plt.subplot(211)#2lignes, 1 col, fig1
    plt.title("nombre de comparaisons (vs. n)")
    plt.plot(n, b,'g-v', label="meilleur")
    plt.plot(n, w, 'r-^', label="pire")
    plt.plot(n, m, 'b-o', label="moyen")
    plt.legend(loc=2) # legende en haut a gche
    
    # echelles log
    plt.subplot(212)
    plt.title("ordre de grandeur des complexites (vs. n)")
    #plt.semilogy()
    plt.ylabel("log(comp)/log(n)")
    plt.plot(n, log(b)/log(n), 'g-v', label="meilleur")
    plt.plot(n, log(w)/log(n), 'r-^', label="pire")
    plt.plot(n, log(m)/log(n), 'b-o', label="moyen")
    plt.legend(loc=4)

    # sortie ecran ou pdf    
    plt.show()
    #pp = PdfPages('./plt-comp-triinsertion.pdf')
    #pp.savefig()
    #pp.close()

testcomp10()
Hide code cell output 
Trions !
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
9 comparaisons pour n =  10
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
45 comparaisons pour n =  10
[14, 91, 1, 52, 87, 23, 33, 17, 9, 38]
[1, 9, 14, 17, 23, 33, 38, 52, 87, 91]
33 comparaisons pour n =  10

testcomp()
Hide code cell output 
Meilleur cas : au plus  9 comparaisons pour n =  10
Pire cas : au moins  45 comparaisons pour n =  10
Moyenne de  10 cas aleatoires :
29 comparaisons pour n =  10
20 comparaisons pour n =  10
26 comparaisons pour n =  10
24 comparaisons pour n =  10
30 comparaisons pour n =  10
22 comparaisons pour n =  10
22 comparaisons pour n =  10
25 comparaisons pour n =  10
25 comparaisons pour n =  10
31 comparaisons pour n =  10
Conclusion :  25 comparaisons en moyenne pour n =  10 ( 10 echantillons)
---------
Meilleur cas : au plus  49 comparaisons pour n =  50
Pire cas : au moins  1225 comparaisons pour n =  50
Moyenne de  10 cas aleatoires :
727 comparaisons pour n =  50
611 comparaisons pour n =  50
683 comparaisons pour n =  50
725 comparaisons pour n =  50
665 comparaisons pour n =  50
673 comparaisons pour n =  50
637 comparaisons pour n =  50
744 comparaisons pour n =  50
610 comparaisons pour n =  50
596 comparaisons pour n =  50
Conclusion :  667 comparaisons en moyenne pour n =  50 ( 10 echantillons)
---------
Meilleur cas : au plus  99 comparaisons pour n =  100
Pire cas : au moins  4950 comparaisons pour n =  100
Moyenne de  10 cas aleatoires :
2496 comparaisons pour n =  100
2290 comparaisons pour n =  100
2528 comparaisons pour n =  100
2620 comparaisons pour n =  100
2497 comparaisons pour n =  100
2315 comparaisons pour n =  100
2495 comparaisons pour n =  100
2473 comparaisons pour n =  100
2433 comparaisons pour n =  100
2583 comparaisons pour n =  100
Conclusion :  2473 comparaisons en moyenne pour n =  100 ( 10 echantillons)
---------
Meilleur cas : au plus  199 comparaisons pour n =  200
Pire cas : au moins  19900 comparaisons pour n =  200
Moyenne de  10 cas aleatoires :
10371 comparaisons pour n =  200
10193 comparaisons pour n =  200
11075 comparaisons pour n =  200
8679 comparaisons pour n =  200
10247 comparaisons pour n =  200
10087 comparaisons pour n =  200
10852 comparaisons pour n =  200
9687 comparaisons pour n =  200
10794 comparaisons pour n =  200
10359 comparaisons pour n =  200
Conclusion :  10234 comparaisons en moyenne pour n =  200 ( 10 echantillons)
---------
Meilleur cas : au plus  299 comparaisons pour n =  300
Pire cas : au moins  44850 comparaisons pour n =  300
Moyenne de  10 cas aleatoires :
22201 comparaisons pour n =  300
22442 comparaisons pour n =  300
22942 comparaisons pour n =  300
22136 comparaisons pour n =  300
23408 comparaisons pour n =  300
22172 comparaisons pour n =  300
22710 comparaisons pour n =  300
23174 comparaisons pour n =  300
23837 comparaisons pour n =  300
22796 comparaisons pour n =  300
Conclusion :  22781 comparaisons en moyenne pour n =  300 ( 10 echantillons)
---------
Meilleur cas : au plus  499 comparaisons pour n =  500
Pire cas : au moins  124750 comparaisons pour n =  500
Moyenne de  10 cas aleatoires :
61288 comparaisons pour n =  500
59169 comparaisons pour n =  500
59289 comparaisons pour n =  500
63808 comparaisons pour n =  500
63461 comparaisons pour n =  500
64150 comparaisons pour n =  500
60316 comparaisons pour n =  500
61954 comparaisons pour n =  500
61560 comparaisons pour n =  500
62918 comparaisons pour n =  500
Conclusion :  61791 comparaisons en moyenne pour n =  500 ( 10 echantillons)
---------
Meilleur cas : au plus  999 comparaisons pour n =  1000
Pire cas : au moins  499500 comparaisons pour n =  1000
Moyenne de  10 cas aleatoires :
255673 comparaisons pour n =  1000
255773 comparaisons pour n =  1000
247521 comparaisons pour n =  1000
252989 comparaisons pour n =  1000
237952 comparaisons pour n =  1000
247932 comparaisons pour n =  1000
260163 comparaisons pour n =  1000
242683 comparaisons pour n =  1000
250927 comparaisons pour n =  1000
251781 comparaisons pour n =  1000
Conclusion :  250339 comparaisons en moyenne pour n =  1000 ( 10 echantillons)
---------

((10, 50, 100, 200, 300, 500, 1000),
 [9, 49, 99, 199, 299, 499, 999],
 [45, 1225, 4950, 19900, 44850, 124750, 499500],
 [25, 667, 2473, 10234, 22781, 61791, 250339])

plottestcomp()

Meilleur cas : au plus  9 comparaisons pour n =  10
Pire cas : au moins  45 comparaisons pour n =  10
Moyenne de  10 cas aleatoires :
24 comparaisons pour n =  10
34 comparaisons pour n =  10
32 comparaisons pour n =  10
27 comparaisons pour n =  10
26 comparaisons pour n =  10
39 comparaisons pour n =  10
26 comparaisons pour n =  10
26 comparaisons pour n =  10
23 comparaisons pour n =  10
30 comparaisons pour n =  10
Conclusion :  28 comparaisons en moyenne pour n =  10 ( 10 echantillons)
---------
Meilleur cas : au plus  49 comparaisons pour n =  50
Pire cas : au moins  1225 comparaisons pour n =  50
Moyenne de  10 cas aleatoires :
661 comparaisons pour n =  50
762 comparaisons pour n =  50
723 comparaisons pour n =  50
707 comparaisons pour n =  50
712 comparaisons pour n =  50
567 comparaisons pour n =  50
691 comparaisons pour n =  50
650 comparaisons pour n =  50
639 comparaisons pour n =  50
582 comparaisons pour n =  50
Conclusion :  669 comparaisons en moyenne pour n =  50 ( 10 echantillons)
---------
Meilleur cas : au plus  99 comparaisons pour n =  100
Pire cas : au moins  4950 comparaisons pour n =  100
Moyenne de  10 cas aleatoires :
2574 comparaisons pour n =  100
2514 comparaisons pour n =  100
2303 comparaisons pour n =  100
2537 comparaisons pour n =  100
2674 comparaisons pour n =  100
2566 comparaisons pour n =  100
2623 comparaisons pour n =  100
2476 comparaisons pour n =  100
2925 comparaisons pour n =  100
2403 comparaisons pour n =  100
Conclusion :  2559 comparaisons en moyenne pour n =  100 ( 10 echantillons)
---------
Meilleur cas : au plus  199 comparaisons pour n =  200
Pire cas : au moins  19900 comparaisons pour n =  200
Moyenne de  10 cas aleatoires :
10739 comparaisons pour n =  200
11267 comparaisons pour n =  200
10381 comparaisons pour n =  200
9649 comparaisons pour n =  200
10014 comparaisons pour n =  200
10562 comparaisons pour n =  200
10331 comparaisons pour n =  200
9621 comparaisons pour n =  200
10308 comparaisons pour n =  200
9978 comparaisons pour n =  200
Conclusion :  10285 comparaisons en moyenne pour n =  200 ( 10 echantillons)
---------
Meilleur cas : au plus  299 comparaisons pour n =  300
Pire cas : au moins  44850 comparaisons pour n =  300
Moyenne de  10 cas aleatoires :
24180 comparaisons pour n =  300
23827 comparaisons pour n =  300
23598 comparaisons pour n =  300
22064 comparaisons pour n =  300
23302 comparaisons pour n =  300
22234 comparaisons pour n =  300
23449 comparaisons pour n =  300
22871 comparaisons pour n =  300
21328 comparaisons pour n =  300
21565 comparaisons pour n =  300
Conclusion :  22841 comparaisons en moyenne pour n =  300 ( 10 echantillons)
---------
Meilleur cas : au plus  499 comparaisons pour n =  500
Pire cas : au moins  124750 comparaisons pour n =  500
Moyenne de  10 cas aleatoires :
65338 comparaisons pour n =  500

61954 comparaisons pour n =  500
63358 comparaisons pour n =  500
60707 comparaisons pour n =  500
60996 comparaisons pour n =  500
60584 comparaisons pour n =  500
63674 comparaisons pour n =  500
62730 comparaisons pour n =  500
61049 comparaisons pour n =  500
63662 comparaisons pour n =  500
Conclusion :  62405 comparaisons en moyenne pour n =  500 ( 10 echantillons)
---------
Meilleur cas : au plus  999 comparaisons pour n =  1000
Pire cas : au moins  499500 comparaisons pour n =  1000
Moyenne de  10 cas aleatoires :
259261 comparaisons pour n =  1000
249523 comparaisons pour n =  1000
246385 comparaisons pour n =  1000
238336 comparaisons pour n =  1000
246411 comparaisons pour n =  1000
243795 comparaisons pour n =  1000
239261 comparaisons pour n =  1000
247880 comparaisons pour n =  1000
235681 comparaisons pour n =  1000
247677 comparaisons pour n =  1000
Conclusion :  245421 comparaisons en moyenne pour n =  1000 ( 10 echantillons)
---------
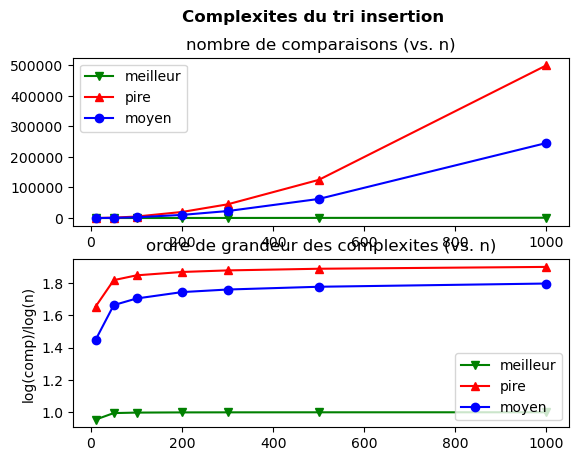
../_images/9373a00b930ce5428fc926d62716d4a4fc402a8206a5d5736fdb0b5c1153c271.png

Interprétation.

Tracé 1 : échelles linéaires en \(n\) et “nombres de comparaisons”

  • Pour les pire cas et le cas moyen, le nombre de comparaisons augmente, de façon visible, plus vite que linéairement.

  • La croissance du meilleur cas est moins claire à cause d’un effet d’échelle (sur l’axe y) induit par le tracé du pire cas.

Tracé 2 : tracés logarithmiques en échelle linéaire

  • le tracé de \(\log(c(n)) / log(n)\) de \(c(n) = n^2\) est la droite horizontale \(y = 2\).

    • \(c(n) = n^2\) donne \(\log(c(n)) = 2 \log(n)\).

  • Avec cette expression, le nombre de comparaisons du pire cas tend bien vers cette droite \(y = 2\),

  • et le cas moyen s’en rapproche.

    • Ce qui traduit bien un nombre de comparaisons quadratique du pire cas du tri insertion.

  • En revanche, le tracé du meilleur cas tend vers \(y = 1\),

    • ce qui s’interprète à juste titre comme un comportement linéaire du meilleur cas du tri insertion.

6.2.5. Vers l’analyse de la complexité#

Le tri insertion se compose de deux boucles imbriquées : for puis while

  • Quel paramètre de la complexité en temps de ce tri ?

  • Quelle mesure de la complexité en temps de ce tri ?

  • Que penser de la boucle while dans le pire cas ?

  • Que penser de la boucle while dans le meilleur cas ?

  • Que penser de la boucle for dans le pire et dans le meilleur cas ?

  • En déduire une expression de la complexité :

    • dans le pire cas

    • dans le meilleur cas

  • En déduire la complexité asymptotique dans le pire cas.

6.3. Tri rapide (ou quicksort)#

  • Un premier exemple de tri (par comparaisons) récursif très efficace en pratique.

  • Introduit par l’informaticien britannique C.A.R Hoare en 1961 (page wikipedia)

6.3.1. Principe#

Ranger une valeur à sa place définitive

  • toutes celles à sa gauche sont plus petites

  • toutes celles à sa droite sont plus grandes

  • ces sous-tableaux gauche et droit ne sont pas (encore) triés

Dans la figure suivante, la valeur v est définitivement bien placée : Illustration de l'invariant du tri rapide

Cette propriété est un invariant du tri rapide.

6.3.2. Récursion#

  1. Hypothèse de départ :

    • on suppose une des valeurs du tableau correctement placée,

      • en t[p] par exemple

    • le tableau initial t[0..n[ est partagé en 2 sous-tableaux :

      • t_gauche[0.. p[ et

      • t_droit[p+1 .. n[

  2. Récursion

    • on trie chacun de ces sous-tableaux en appliquant le même principe

  3. Terminaison : un sous-tableau trié

    • le sous-tableau est de taille 1 :

    • réduit à 1 élément == pivot == bien placé

6.3.3. Principe de mise en oeuvre avec duplication du tableau t#

Une première mise en oeuvre “à vocation pédagogique” s’appuie sur la duplication du tableau de valeurs à chaque étape de la récursion.

Etape 1 : placer correctement le pivot v

  • parcourir et comparer chaque élément t[i] avec v

  • si t[i] < v, laisser t[i] à gauche de v

  • sinon déplacer t[i] à droite de v invariant du tri rapide

En pratique,

  • le choix du pivot est arbitraire :

    • t[0] par exemple dans la suite

  • les déplacement peuvent être réalisés avec 2 tableaux (par exemple) :

    • tableau source \(\to\) tableau destination

    • On remplit le tableau destination par chacun de ses 2 bouts

    • et on place t[0] à la fin. avec 2 tableaux

Etape 2 : récursion sur chacun des deux sous-tableaux gauche et droit

Le premier pivot (t[0] ici) est correctement placé. pivot

La récursion sur chacun des deux sous-tableaux gauche et droit permet de placer correctement les 2 nouveaux pivots t[*].
recursion

  • t[*] peuvent à nouveau être “les t[0]” de chacun des sous-tableaux.

Exemple#

On déroule à la main ce tri rapide pour trier le tableau t= [4,3,5,8,2,6,7].

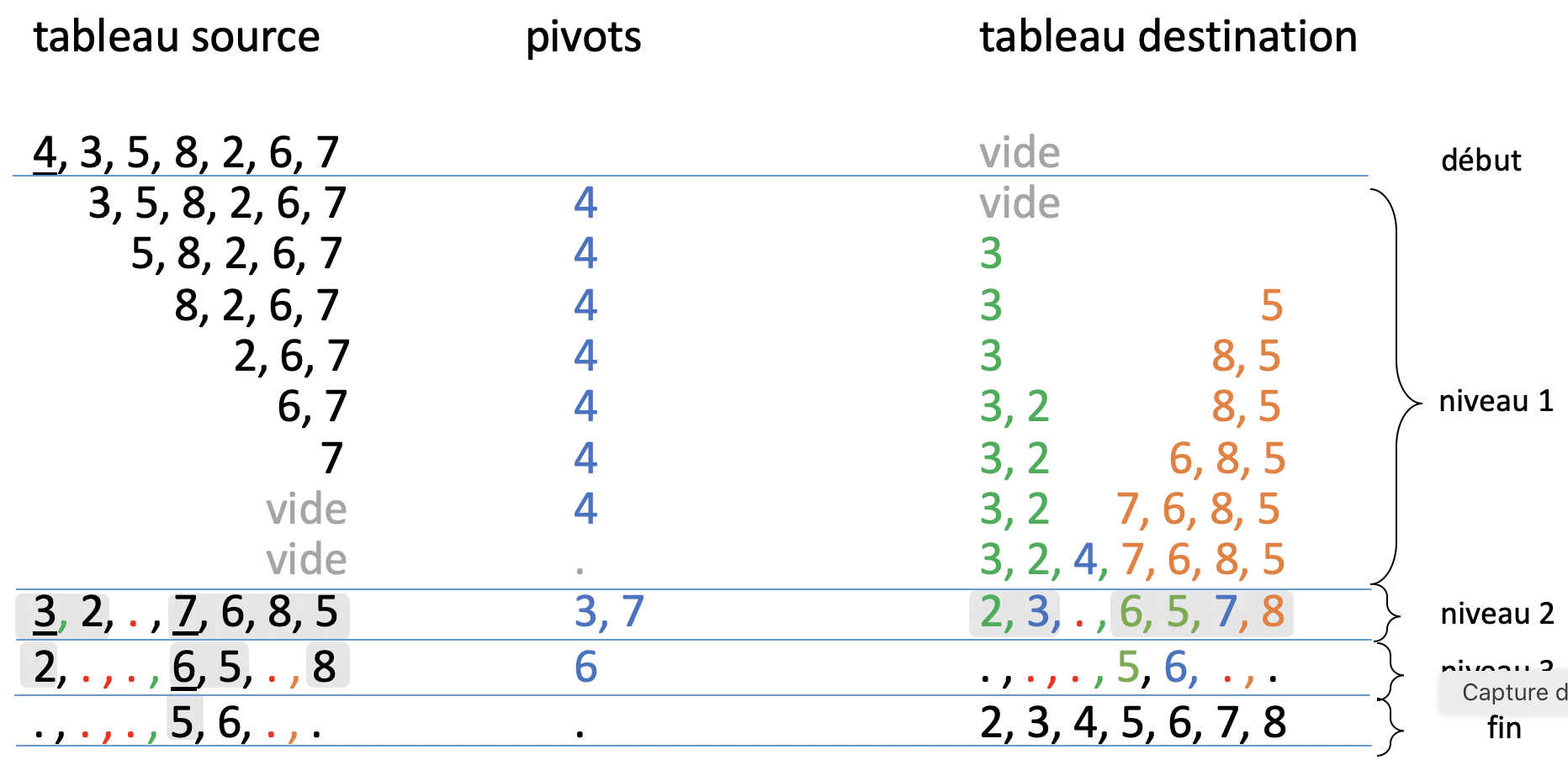
exemple

6.3.4. Mise en oeuvre en place#

Le principe étant bien compris, on effectue un traitement équivalent en place, c-a-d. sans dupliquer le tableau de valeurs.

Rmq: Les valeurs entre [.] sont les numéros de ligne dans le code de partition qui suit.
Hélas les numéros de lignes n’apparaissent pas dans la version html ; le def est en ligne 1, le assert en ligne 10 … et le return en ligne 23.

  1. une fonction partition organise le sous-tableau t[g..d[ comme suit.

    • [11] on choisit t[d-1] comme pivot (autre choix arbitraire)

    • [21] à la fin de l’itération, il se retrouvera en t[m]

    • l’indice m va partitionner le tableau en 2 parties : à gauche, les valeurs inférieures ou égales au pivot, à droite, à partir de m+1, les valeurs strictement supérieures

      • [13] pour cela, on parcourt t de g vers d-1 (d-1 exclus)

      • [12] on initialise m = g : si le pivot est la plus petite valeur de t[g,d[ alors il doit finir en t[g]

      • [15:17] on permute chaque valeur rencontrée plus petite que le pivot avec t[m], et

      • [18] m est incrémenté car le nombre de valeurs inférieures au pivot vient d’être augmenté de 1

        • m reste (pour l’instant) l’indice de la première valeur strictement supérieure au pivot :

        • ainsi m est l’indice qui sépare les 2 partitions gche (valeurs plus petites ou égales que le pivot) et droite (plus grandes) de t

      • [20] et une fois arrivé en d-1, on permute t[m] et le pivot :

        • le pivot se retrouve en t[m], ce qui conserve la partition “gauche-droite” et correspond à l’objectif

    • remarque : la fonction retourne la valeur de séparation m

    • remarque : ce traitement s’effectue en place : pas la peine de renvoyer le tableau

  1. la récursion trirapide0( ) appelle (récursivement) partition() sur les 2 sous-tableaux délimités de façon exclusive par m (cad t[g,m[ et t[m+1,d[), et ce tant que leur longueur est plus grande que 1 ; sinon terminaison

  1. la fonction trirapide() réalise l’appel principal sur le tableau complet t[g,d[ :

    • soit l’appel pour g==0 et d==len(t)

def partition(t: list[int], g: int, d: int) -> int:
    """partitionne t[g,d[
    invariant : avant la boucle i
    si g<=k < m, t[k] <= pivot
    si m+1<=k <= i-1, t[k]  > pivot
    **** choix arbitraire: t[d-1] = pivot. 
    Cad : t[g,m] <= pivot < t[m+1,d[ (*)
    avec pivot = t[m]
    et m+1 indice du premier > pivot"""
    assert g < d-1 # t contient au moins 2 éléments
    
    pivot = t[d-1]
    m = g
    for i in range(g, d-1): # d-1 non atteint
        if t[i] <= pivot: 
            tmp = t[i] # permuter t[m] et t[i]
            t[i] = t[m]
            t[m] = tmp
            m = m+1 # m attend le prochain <= pivot
    # placer pivot a sa place definitive
    t[d-1] = t[m] 
    t[m] = pivot
    #print("partition :", t[g:d])
    return m

def trirapide0(t: list[int], g: int, d: int) -> None:
    '''partitionne t[g,d[ 
    et appels récursifs sur t[g,m[ et t[m+1,d['''
    if d - g > 1: #il reste au moins 2 elmnts ds cette sous-partie de t
        m = partition(t, g, d)
        trirapide0(t, g, m-1) 
        trirapide0(t, m+1, d)  

def trirapide(t: list[int], n: int) -> None:
    '''tri rapide de t[0, len(t)['''
    trirapide0(t, 0, len(t)) 

#t = tabalea(10)
t = [15,4,2,8,17,23,0,1]
print("avant :", t)
trirapide(t, len(t))
print("après :", t)

avant : [15, 4, 2, 8, 17, 23, 0, 1]
après : [0, 1, 2, 4, 8, 15, 17, 23]

6.3.5. Exercices#

  • Ecrire une version (partition2) plus simple avec duplication du tableau

  • Ecrire une version qui affiche les évolutions successives de t après chaque pivot

6.3.6. Corrections#

Sauter ce passage en première lecture

Hide code cell content 
def partition2(t, n, g, d):
    '''Quicksort avec duplication tableaux
    partitionne t[g, d[ autour du pivot (ici l élément de gauche t[g])
    retourne la position finale du pivot'''
    assert g < d
    # on définit t_cible et on place les indices à ses 2 bouts
    i = g
    j = d-1
    # choix arbitraire du pivot
    pivot = t[g]
    # on y va
    for k in range(g+1, d): 
        if t[k] <= pivot: 
            t_cible[i] = t[k] # on remplit t_cible par la gauche 
            i = i + 1  
        else: 
            t_cible[j] = t[k] # on remplit t_cible par la droite
            j = j - 1  
    # on peut placer le pivot à la place qui reste
    assert i == j
    m = i
    t_cible[m] = pivot
    
    # on met à jour t[g,d[ à l aide de t_cible
    t[g:d]  = [t_cible[i] for i in range(g,d)]
    print("partition [g, d[:m -> [", g, ',' , d,"[:", m,  t_cible[g:d], t[g:d])

    return m
Hide code cell content 
def triRapideRec2(t, g, d):
    if d - g > 1: #il reste au moins 2 elmnts ds cette sous-partie de t
        m = partition2(t, len(t), g, d)       
        triRapideRec2(t, g, m) # m est exclu
        triRapideRec2(t, m+1, d)

def trirapide2(t):
    global t_cible # bien noter le global !!
    t_cible = [0 for i in range(len(t))]
    print("dem :", t_cible, t)
    triRapideRec2(t, 0, len(t))
Hide code cell content 
t = tabalea(7)
print("avant :", t)
trirapide2(t)
print("après :", t)

avant : [41, 71, 53, 75, 22, 72, 50]
dem : [0, 0, 0, 0, 0, 0, 0] [41, 71, 53, 75, 22, 72, 50]
partition [g, d[:m -> [ 0 , 7 [: 1 [22, 41, 50, 72, 75, 53, 71] [22, 41, 50, 72, 75, 53, 71]
partition [g, d[:m -> [ 2 , 7 [: 2 [50, 71, 53, 75, 72] [50, 71, 53, 75, 72]
partition [g, d[:m -> [ 3 , 7 [: 4 [53, 71, 72, 75] [53, 71, 72, 75]
partition [g, d[:m -> [ 5 , 7 [: 5 [72, 75] [72, 75]
après : [22, 41, 50, 53, 71, 72, 75]

6.3.7. Performances, pire cas, meilleur cas#

S’inspirer de la démarche sur triInsertion( ) avec les exercices suivants. Bon travail !

Exercices#

  • Ecrire une version qui compte le nombre de comparaisons

  • Générer le pire cas , et le meilleur cas, puis vérifier

Hide code cell content 
def partitionCompte(t, g, d):
    """version avec decompte nbre comp :"""
    global nb 
    assert g < d-1 # t contient au moins 2 éléments
    pivot = t[d-1]
    m = g
    for i in range(g, d-1): # d-1 non atteint
        nb = nb + 1
        if t[i] <= pivot: 
            tmp = t[i] # permuter t[m] et t[i]
            t[i] = t[m]
            t[m] = tmp
            m = m+1 # m attend le prochain <= pivot
    # placer pivot a sa place definitive
    t[d-1] = t[m] 
    t[m] = pivot
    #print("partition :", t[g:d])
    print("m:", m)
    return m

def trirapide0Compte(t, g, d):
    """version avec decompte nbre comp :"""
    if d - g > 1: #il reste au moins 2 elmnts ds cette sous-partie de t
        m = partitionCompte(t, g, d)
        trirapide0Compte(t, g, m-1) 
        trirapide0Compte(t, m+1, d)

def trirapideCompte(t):
    '''version avec decompte nbre comp :
    tri rapide de t[0, len(t)['''
    global nb
    nb = 0
    trirapide0Compte(t, 0, len(t))
    return nb
Hide code cell content 
#t = tabalea(10)
t = [15,4,2,8,17,23,0,1]
print("avant :", t)
nbcomp = trirapideCompte(t)
print("après :", t)
print("nb comparaisons :", nbcomp)

print("* Pire cas : ")
#t_pire = [i for i in range(7,-1,-1)]
t_pire = [1, 2, 3, 4, 5, 6, 7, 0]
print("avant :", t_pire)
nbcomp = trirapideCompte(t_pire)
print("après :", t_pire)
print("nb comparaisons :", nbcomp)

print("* Meilleur cas : ")
t_best = [0, 2, 1 , 5, 6,  4, 3]
print("avant :", t_best)
nbcomp = trirapideCompte(t_best)
print("après :", t_best)
print("nb comparaisons :", nbcomp)

avant : [15, 4, 2, 8, 17, 23, 0, 1]
m: 1
m: 3
m: 4
m: 6
après : [0, 1, 2, 4, 8, 15, 17, 23]
nb comparaisons : 17
* Pire cas : 
avant : [1, 2, 3, 4, 5, 6, 7, 0]
m: 0
m: 1
m: 2
m: 3
m: 4
m: 5
m: 6
après : [0, 1, 2, 3, 4, 5, 6, 7]
nb comparaisons : 28
* Meilleur cas : 
avant : [0, 2, 1, 5, 6, 4, 3]
m: 3
m: 1
m: 5
après : [0, 2, 1, 3, 4, 5, 6]
nb comparaisons : 9

6.3.8. Vers l’analyse de la complexité#

Le tri rapide :

  • consiste en des appels récursifs qui effectuent des partitions successives (en 2 sous-tableaux de taille strictement inférieure) jusqu’à terminaison (sous-tableau de taille 1 ou 0).

  • Chacune de ces partitions permet de placer correctement le pivot associé.

Les questions suivantes guident l’analyse de la complexité du pire et du meilleur cas de cet algorithme.

  • Quel paramètre de la complexité en temps de ce tri ?

  • Quelle mesure de la complexité en temps de ce tri ?

  • Analyse du pire cas :

    • Que penser de la taille des sous-tableaux à chaque appel récursif ?

    • Combien d’appels récursifs sont nécessaires au traitement de ce pire cas ?

    • Expliciter une relation de récurrence sur \(C(n)\) la complexité de la partition d’un tableau de taille \(n\) dans le pire cas

    • Expliciter \(C(1)\) la complexité de la partition d’un tableau de taille \(1\)

    • En déduire \(C(n)\) la complexité du tri rapide dans le pire cas ?

  • Analyse du meilleur cas :

    • Que penser de la taille des sous-tableaux à appel récursif ?

    • Combien d’appels récursifs au plus (*) sont nécessaires au traitement de ce meilleur cas ? (*): Il est commode de ramener les tailles des (sous-)tableaux à des puissances de 2. On commence par exemple avec \(n = 2^p\) valeurs à trier.

    • Expliciter une relation de récurrence sur \(C(n)\) la complexité de la partition d’un tableau de taille \(n\) dans le meilleur cas

    • Expliciter \(C(1)\) la complexité de la partition d’un tableau de taille \(1\)

    • En déduire \(C(n)\) la complexité du tri rapide dans le meilleur cas ?

  • A partir de ces deux cas, que penser du tri rapide ?

  • En déduire les complexités asymptotiques des meilleurs et pires cas.

6.4. Tri fusion#

Un exemple de tri de complexité optimale (semi-logarithmique : \(n\log(n)\)) issu de la stratégie diviser pour régner.

6.4.1. Principe#

  1. Fusionner 2 tableaux triés pour obtenir un tableau unique trié

  • Facile : il suffit de répéter la comparaison du premier élément de chacun des 2 tableaux.

  1. Obtenir 2 tableaux triés ? Récursion

  • on divise le tableau t[0..n[ en 2 sous-tableaux de taille moitié : par exemple

    • t_gauche[0..n//2[ et

    • t_droit[n//2..n[

  • on trie chacun de ces sous-tableaux en appliquant le même principe.

  1. Terminaison : un sous-tableau trié.

  • le sous-tableau est de taille 1 : réduit à 1 élément

La figure suivante illustre ce principe. 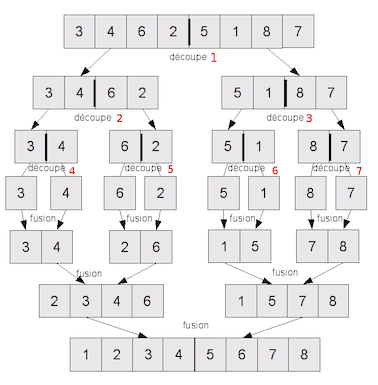source openclassroom (source openclassroom)

La forme récursive du tri fusion est issue d’une stratégie “diviser pour régner” similaire à celle utilisée pour la recherche dichotomique. En pratique, les appels récursifs définissent les moitiés de tableaux à manipuler. Le “coeur” de l’algorithme est donc la phase de fusion que nous détaillons maintenant.

6.4.2. Exemple de la fusion de 2 tableaux triés#

On illustre la fusion de 2 tableaux triés quelconques à l’aide de l’exemple suivant.

Fusionnons les 8 valeurs stockées dans les tableaux triés t_g =  [1,3,5,8,11] et t_d = [2,6,7].

Rmq. La récursion du tri fusion conduirait ici à 2 tableaux triés de taille 4 chacun.

Fusion

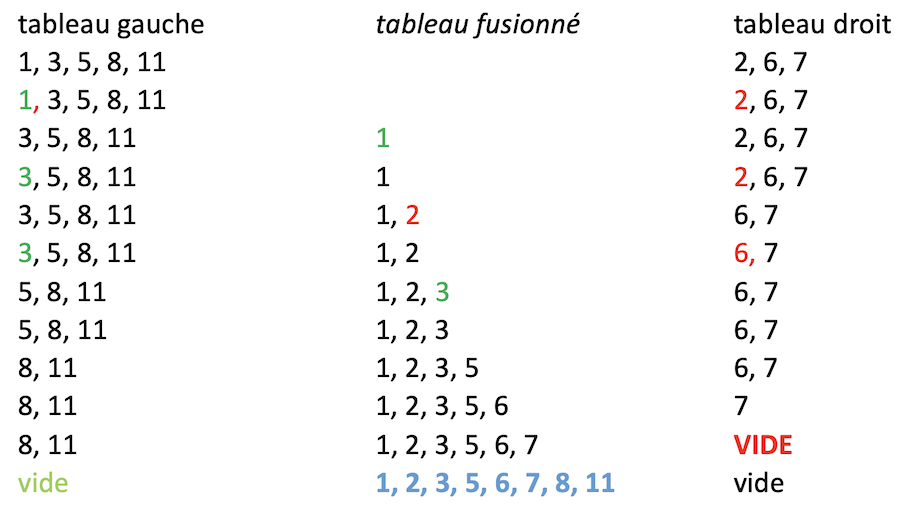
Fusionner 2 tableaux triés

6.4.3. Algorithme : analyse et (une) écriture#

Fusion#

Entrées : 2 tableaux t1 et t2, de longueurs n1 et n2, triés
Sortie : 1 tableau t de taille n1+n2 qui sera trié

Plusieurs cas de figures sont possibles.

  1. Les entrées t1 et t2 sont :

    • des tableaux distincts,

    • ou des sous-tableaux d’un unique tableau t en connaissant l’indice dans t de séparation des valeurs de t1 et t2.

  2. La fusion peut :

    • créer et retourner un nouveau tableau t ; et ainsi “oublier” t1 et t2 après la fusion ce qui est facile mais coûteux en mémoire :),

    • ou utiliser 2 “grands tableaux” passés par l’utilisateur,

    • ou utiliser une copie locale.

On effectue les choix suivants.

  • Les entrées t1 et t2 sont des sous-tableaux d’un unique tableau a[g, d[ passé en paramètre.

    • L’indice de séparation est donné comme paramètre m.

  • La sortie est un second tableau b aussi passé en paramètre.

  • La fusion est donc une procédure qui modifie b.

def fusion(a: list[int], b: list[int], g: int, m: int, d: int) -> None:
    """ fusion des 2 moitiés du tableau a en le tableau b.
    a et b sont passés en arguments (pas de copie locale, pas de return) : on prend dans a, on range dans b.
    entrées. a, b : 2 tableaux (de même taille).
    g, m, d : le sous-tab gauche est a[g,m[, celui de droite est a[m,d[
    sortie. b[g,d[ trié.
    """
    assert len(a)==len(b) # a[] et b[] sont de la même taille
    
    i, j = g, m           # i et j parcourent resp. les partie G et D de a[]
    for k in range(g, d): # k parcourt b[] de g à d-1
        if i < m and (j==d or a[i] < a[j]):
            # G n est pas vide
            b[k] = a[i]
            i = i+1
        else:
            b[k] = a[j]
            j = j+1
            
    return None 

t_in  = [2*i for i in range(5)] + [2*i+1 for i in range(5)]
t_out = [0 for i in range(10)]
print(t_in, t_out)

fusion(t_in, t_out, 0, 5, 10)

print(t_in, t_out)

[0, 2, 4, 6, 8, 1, 3, 5, 7, 9] [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 2, 4, 6, 8, 1, 3, 5, 7, 9] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Rmq. Ce choix de fusion() conduit à dupliquer l’espace mémoire nécessaire au stockage des valeurs à trier. Ainsi cette version ne conduit pas à une version en place du tri fusion. Il est possible de mettre en oeuvre une version en place (en gérant les déplacements des valeurs fusionnées dans un sous-tableau fixé). Une telle solution est un peu délicate à écrire et, surtout, assez inefficace en pratique comparée à la solution avec duplication.

En première lecture, sauter la section suivante et aller en section 4.4 _Diviser pour régner._

Analyse plus détaillée de la programmation de la fusion#

Affichons les états successifs du tableau fusionné.

def fusionPrint(a: list[int], b: list[int], g: int, m: int, d: int) -> None:
    """ version avec affichages de :
    fusion avec deux tableaux a et b passés en arguments
    (pas de copie locale, pas de return) : on prend dans a, on range dans b.
    entrées. a, b : 2 tableaux (de même taille).
    g, m, d : le sous-tab gauche est a[g,m-1], celui de droite est a[m,d-1]
    sortie. b[g,d] trié.
    """
    assert len(a)==len(b) # a[] et b[] sont de la même taille
    
    i, j = g, m           # i et j parcourent resp. les partie G et D de a[]
    for k in range(g, d): # k parcourt b[] de g à d-1
        if i < m and (j==d or a[i] < a[j]):
            # G n est pas vide
            b[k] = a[i]
            i = i+1
        else:
            b[k] = a[j]
            j = j+1
        print(k, ": ", b)
        
    return None

t_in  = [2*i for i in range(5)] + [2*i+1 for i in range(5)]
t_out = [0 for i in range(10)]
print(t_in)
fusionPrint(t_in, t_out, 0, 5, 10)
print(t_out)

[0, 2, 4, 6, 8, 1, 3, 5, 7, 9]
0 :  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 :  [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
2 :  [0, 1, 2, 0, 0, 0, 0, 0, 0, 0]
3 :  [0, 1, 2, 3, 0, 0, 0, 0, 0, 0]
4 :  [0, 1, 2, 3, 4, 0, 0, 0, 0, 0]
5 :  [0, 1, 2, 3, 4, 5, 0, 0, 0, 0]
6 :  [0, 1, 2, 3, 4, 5, 6, 0, 0, 0]
7 :  [0, 1, 2, 3, 4, 5, 6, 7, 0, 0]
8 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
9 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Petite amélioration#

On voit ce qui se passe à chaque itération. Ce qui va permettre de constater qu’on traite inutilement des sous-tableaux vides.

t_in  = [i for i in range(10)]
print(t_in)
t_out = [0 for i in range(10)]
fusionPrint(t_in, t_out, 0, 5, 10)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
0 :  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 :  [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
2 :  [0, 1, 2, 0, 0, 0, 0, 0, 0, 0]
3 :  [0, 1, 2, 3, 0, 0, 0, 0, 0, 0]
4 :  [0, 1, 2, 3, 4, 0, 0, 0, 0, 0]
5 :  [0, 1, 2, 3, 4, 5, 0, 0, 0, 0]
6 :  [0, 1, 2, 3, 4, 5, 6, 0, 0, 0]
7 :  [0, 1, 2, 3, 4, 5, 6, 7, 0, 0]
8 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
9 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Pourquoi ces appels inutiles ?

Exercice : Proposer un palliatif !

Comment arrêter les parcours des (sous)-tableaux ?
Objectif : ne pas aller inutilement jusqu’au bout d’un sous-tableau alors que l’autre est vide.

Plusieurs choix aussi :

  1. en gérant les indices de façon adaptée

  • à la manière du contrôle j == d dans fusion() qui indique si le tableau droit est vide

  1. en introduisant des sentinelles : valeurs choisies pour arrêter les itérations

  • exemple : une très grande valeur (un “infini”) si on trie par ordre croissant

Exercice de programmation#

Une seule version avec et sans affichage

def fusion(a: list[int], b: list[int], g: int, m: int, d: int, verb=False) -> None:
    """ version avec choix d'affichage de :
    fusion avec deux tableaux a et b passés en arguments
    (pas de copie locale, pas de return) : on prend dans a, on range dans b.
    entrées. a, b : 2 tableaux (de même taille).
    g, m, d : le sous-tab gauche est a[g,m-1], celui de droite est a[m,d-1]
    sortie. b[g,d] trié.
    """
    assert len(a)==len(b) # a[] et b[] sont de la même taille
    
    i, j = g, m           # i et j parcourent resp. les partie G et D de a[]
    for k in range(g, d): # k parcourt b[] de g à d-1
        if i < m and (j==d or a[i] < a[j]):
            # G n est pas vide
            b[k] = a[i]
            i = i+1
        else:
            b[k] = a[j]
            j = j+1
        if verb == True:
            print(k, ": ", b)
        
    return None
            

t = [i for i in range(10)]
tt = [0 for i in range (10)]

fusion(t, tt, 0, 5, 10)
print("sans affichage", tt)
tt = [0 for i in range (10)]

print("avec affichages")
fusion(t, tt, 0, 5, 10, True)

sans affichage [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
avec affichages
0 :  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 :  [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
2 :  [0, 1, 2, 0, 0, 0, 0, 0, 0, 0]
3 :  [0, 1, 2, 3, 0, 0, 0, 0, 0, 0]
4 :  [0, 1, 2, 3, 4, 0, 0, 0, 0, 0]
5 :  [0, 1, 2, 3, 4, 5, 0, 0, 0, 0]
6 :  [0, 1, 2, 3, 4, 5, 6, 0, 0, 0]
7 :  [0, 1, 2, 3, 4, 5, 6, 7, 0, 0]
8 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
9 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

6.4.4. Diviser pour régner#

L’algorithme complet du tri fusion peut maintenant s’écrire à partir de l’analyse “diviser pour régner” appliquée au tableau à trier.

  • Principe récursif de division en 2 parties de taille moitié jusqu’à obtenir un tableau de longueur 0 ou 1

  • terminaison :

    • tableau vide (longueur 0) : g >= d

    • tableau de longueur 1 : g == d-1

def trifusion(a: list[int], dim_a: int) -> None:
    """tri fusion qui utilise fusion(a,b,g,m,d)
    avec une fonction récursive locale pour travailler sur 1 seul tableau"""
    b = a[:] # copie de a
    
    # fonction recursive locale
    def trifusion_rec(g: int, d: int):
        if g  >= d-1 : # 0 ou 1 éléments
            return        
        m = (g+d)//2
        trifusion_rec(g, m)
        trifusion_rec(m, d)
        b[g:d] = a[g:d]
        fusion(b, a, g, m, d)
        
    # appel principal
    trifusion_rec(0, len(a))
    #
    return None

t  = [2*i for i in range(4)] + [2*i+1 for i in range(4)]
print(t)
trifusion(t, len(t))
print(t)

[0, 2, 4, 6, 1, 3, 5, 7]
[0, 1, 2, 3, 4, 5, 6, 7]

A venir : le même principe “divise pour régner” avec des variations d’implémentation.

6.4.5. Performances, pire cas, meilleur cas#

S’inspirer des démarches précédentes. Bon travail !

Hide code cell content 
def fusionOpt(a, b, g, m, d, verb=False, compteFusion=False):
    """ version avec choix d'affichage et decompte comparaison de :
    fusion avec deux tableaux a et b passés en arguments
    (pas de copie locale, pas de return) : on prend dans a, on range dans b.
    entrées. a, b : 2 tableaux (de même taille).
    g, m, d : le sous-tab gauche est a[g,m-1], celui de droite est a[m,d-1]
    sortie. b[g,d] trié.
    """
    global nb # pour le decompte des comparaisons
    assert len(a)==len(b) # a[] et b[] sont de la même taille
    i, j = g, m           # i et j parcourent resp. les partie G et D de a[]
    for k in range(g, d): # k parcourt b[] de g à d-1
        if compteFusion == True:
            nb = nb + 1
        if i < m and (j==d or a[i] < a[j]):
            # G n est pas vide
            b[k] = a[i]
            i = i+1
        else:
            b[k] = a[j]
            j = j+1
        if verb == True:
            print(k, ": ", b)
            
t = [i for i in range(10)]
tt = [0 for i in range (10)]

fusionOpt(t, tt, 0, 5, 10)
print("sans affichage", tt)
tt = [0 for i in range (10)]

print("avec affichages")
fusionOpt(t, tt, 0, 5, 10, True)

sans affichage [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
avec affichages
0 :  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 :  [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
2 :  [0, 1, 2, 0, 0, 0, 0, 0, 0, 0]
3 :  [0, 1, 2, 3, 0, 0, 0, 0, 0, 0]
4 :  [0, 1, 2, 3, 4, 0, 0, 0, 0, 0]
5 :  [0, 1, 2, 3, 4, 5, 0, 0, 0, 0]
6 :  [0, 1, 2, 3, 4, 5, 6, 0, 0, 0]
7 :  [0, 1, 2, 3, 4, 5, 6, 7, 0, 0]
8 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 0]
9 :  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Hide code cell content 
def trifusionOpt(a, dim_a, compte=False):
    """version avec decompte comparaisons de 
    tri fusion qui utilise fusion(a,b,g,m,d)
    avec une fonction récursive locale pour travailler sur 1 seul tableau"""
    if compte == True:
        global nb 
        nb = 0
    b = a[:] # copie de a
    # fonction recursive locale
    def trifusion_rec(g, d):
        if g  >= d - 1: # 0 ou 1 éléments
            return        
        m = (g+d)//2
        trifusion_rec(g, m)
        trifusion_rec(m, d)
        b[g:d] = a[g:d]
        fusionOpt(b, a, g, m, d, compteFusion=compte)
    # appel principal
    trifusion_rec(0, len(a))
    #
    if compte == True:
        return nb
Hide code cell content 
from random import randint 
t_best = [randint(0,8) for i in range(8)]
t_pire = [randint(0,8) for i in range(8)]
print(t_best, t_pire)
nbcomp = trifusionOpt(t_best, len(t), True)
print(t_best)
print("nb comparaisons:", nbcomp)
nbcomp = trifusionOpt(t_pire, len(t), True)
print(t_pire)
print("nb comparaisons:", nbcomp)

[3, 2, 2, 8, 2, 4, 1, 0] [3, 6, 7, 4, 4, 8, 6, 2]
[0, 1, 2, 2, 2, 3, 4, 8]
nb comparaisons: 24
[2, 3, 4, 4, 6, 6, 7, 8]
nb comparaisons: 24

6.4.6. Vers l’analyse de la complexité#

Le tri fusion consiste en des appels récursifs qui :

  • effectuent des partitions successives en 2 sous-tableaux de taille moitié jusqu’à terminaison (sous-tableau de taille 1 ou 0 donc trié),

  • puis des fusions de sous-tableaux triés en un tableau trié de longueur double.

Ainsi, la dernière fusion construit le tableau complet trié.

Les questions suivantes guident l’analyse de la complexité du pire et du meilleur cas de cet algorithme.

  • Quel paramètre de la complexité en temps de ce tri ?

  • Quelle mesure de la complexité en temps de ce tri ?

  • Analyse pour \(n = 2^p\) valeurs à trier.

    • Que penser de la taille des sous-tableaux à chaque appel récursif ?

    • Combien d’appels récursifs sont nécessaires à la terminaison des appels récursifs ?

    • Pour \(n\) ainsi fixé, que penser d’un pire cas et d’un meilleur cas ?

    • Expliciter une relation de récurrence sur \(C(n)\) la complexité du tri fusion d’un tableau de taille \(n= 2^p\)

    • Expliciter \(C(1)\) la complexité du tri fusion d’un tableau de taille \(2^0=1\)

    • En déduire \(C(n)\) la complexité du tri fusion ?

  • Que penser du tri rapide ?

  • En déduire le complexité asymptotique du tri fusion.

6.5. Complexités de ces algorithmes de tri#

On synthétise les différents résultats de complexité de ces algorithmes de tri.

Complexité

Tri insertion

Tri rapide

Tri fusion

en mémoire

tri en place

tri en place

NON pas ici

en temps : pire cas

quadratique : \(\cal{O}(n^2)\)

quadratique: \(\cal{O}(n^2)\)

semi-logarithmique: \(\cal{O}(n\log(n))\)

.

double boucle imbriquée for-while complètes

\(C(n) = n-1 + C(n-1)\) \(C(1)=0\)

\(C(n) = C(n/2) + f(n)\) \(\text{fusion}: f(n)=n-1\)

en temps : meilleur cas

linéaire : \(\cal{O}(n)\)

semi-logarithmique: \(\cal{O}(n\log(n))\)

semi-logarithmique: \(\cal{O}(n\log(n))\)

.

boucle interne while vide

\(C(n) = (n-1) + 2\times C(n/2)\) \(C(1)=0\)

\(C(n) = C(n/2) + f(n)\) \(\text{fusion}: f(n)=n/2\)

en temps : cas moyen

quadratique : \(\cal{O}(n^2)\)

semi-logarithmique: \(\cal{O}(n\log(n))\)

semi-logarithmique: \(\cal{O}(n\log(n))\)

6.6. (\(\star\)) Prouver la correction de ces algorithmes de tri#

On explicite les invariants des algorithmes présentés dans ce chapitre. On laisse en exercice la preuve de ces invariants.

6.6.1. Tri insertion#

(P) Avant l’itération i, le sous-tableau t[0, i[ est trié.

6.6.2. Tri rapide (quicksort)#

Invariant de partition(t, g, d) :

au début de l’itération \(i\) : pour tout \(k\) dans \([g, d[\), on a :

  • si \(g \le k \le m\) alors \(t[k] \le v\),

  • si \(m+1 \le k < i\) alors \(t[k] > v\),

  • si \(g = d-1\) alors \(t[k] = v.\)

Remarque : on ne dit rien sur la tranche \(t[i, d-1[\) qui sont a priori quelconques.

6.6.3. Tri fusion#

Invariant de la boucle for dans fusion(t, g, m, d) :

au début de l’itération \(k\) :

  • le sous-tableau \(t[g, k[\) contient en ordre trié les \((k-g)\) plus petits éléments de \(G[0, m-g[\) et \(D[0, d-m[\) ;

  • \(G[i1]\) et \(D[i2]\) sont les plus petits éléments respectifs de G et D a ne pas avoir été copiés dans t.

6.7. Conclusion#

  • Trois algorithmes de tris de complexités différentes

    • pires cas, meilleurs cas

    • cas moyen pour le tri rapide

  • Mises en oeuvre “naturelles” différentes : itératif vs récursif

  • Exemples d’application du paradigme “diviser pour régner”

  • Exemples d’invariant

    • pour prouver la correction de l’algorithme

Contents