Ctrl+K

Modules utiles

13. Modules utiles#

Mis à jour : May 15, 2025, lecture : 8 minutes minimum, PhL.

random, matplotlib et time pour des expériences de complexité, entre autres.

Petites expériences qui nous permettent de découvrir des modules bien utiles :

  • d’introduire de l’aléatoire avec random

    • pour générer des données de test, de débug, …

  • d’apprendre à faire des graphiques avec matplotlib

  • d’utiliser des fonctions de modules importés du module time pour mesurer des temps d’exécution,

    • et ainsi apprécier la validité et les limites de la notion de complexité algorithmique,

13.1. De l’aléa avec le module random#

Commençons par ce module déjà utilisé au semestre 1.

Les expérimentations demandent souvent mais pas systématiquement de générer des données aléatoires.
Le module random permet ça, ou presque car la génération déterministe de valeurs a priori quelconques est un processus pseudo-aléatoire .

13.1.1. Principe d’un générateur pseudo-aléatoire#

  • une graine : \(u_0\)

  • une récurrence déterministe : \(u_n = f(u_{n-1})\) où \(f\) définit de l’aléa.

13.1.2. Fonctions utiles#

Après un :

import random

  • random.seed() : graine du générateur

    • fixer la graine permet la reproductibilité de la génération pseudo-aléatoire

Lois discrètes (entières)

  • random.randint(a, b) : uniforme discrète sur [a, b] <– remarquer l’intervalle fermé !

  • random.randrange(a, b, pas) : uniforme discrète sur [a, a+pas, a+2*pas, …, b[ (intervalle ouvert à droite)

Lois continues

  • random.random() : uniforme sur [0,1]

  • random.uniform(a, b) : uniforme sur [a,b]

  • random.gauss(moyenne, ecart_type) : Normal(\(\mu\), \(\sigma\))

#help(random)

n = 10
t0 = [0 for i in range(n)]
t1 = [0 for i in range(n)]
t2 = [0 for i in range(n)]
t3 = [0 for i in range(n)]

# graine arbitrairement choisie par le système 
random.seed()
for i in range(10):
    t0[i] = random.random()

for i in range(10):
    t1[i] = random.random()

# on bloque la graine
random.seed(12345)
for i in range(10):
    t2[i] = random.random()

# on reprend la même graine 
random.seed(12345)
for i in range(10):
    t3[i] = random.random()

print(t0 == t1)
print(t1 == t2)
print(t2 == t3)
print(t1)
print(t2)

False
False
True
[0.2559961598230419, 0.24918513880707738, 0.26136002419556403, 0.6043984329879423, 0.8009794965765402, 0.7085994182467212, 0.20334106235334415, 0.45851235313522987, 0.647319708685299, 0.7647039412902213]
[0.41661987254534116, 0.010169169457068361, 0.8252065092537432, 0.2986398551995928, 0.3684116894884757, 0.19366134904507426, 0.5660081687288613, 0.1616878239293682, 0.12426688428353017, 0.4329362680099159]

13.2. Tracer avec matplotlib#

C’est utile … et pas moche !

13.2.1. matplotlib : qu’est ce que ça fait ?#

Le module python matplotlib est un module adapté à tous les types de tracés scientifiques : courbes, histogrammes, nuages de points, \(\dots\) On verra même qu’il permet d’afficher des images, ds photos, …

  • Ses options sont très nombreuses, de même que la documentation en ligne ou “livrée avec”. matplotlib est composé de nombreux sous-modules. Parmi ceux-ci, celui qui nous intéresse est pyplot.
    L’instruction suivante est très très classique.

import matplotlib.pyplot as plt

  • L’utilisation basique de pyplot consiste :

    • à tracer des courbes \(x-y\)

    • à partir de listes de points, d’un fichier de valeurs ou d’une expression,

    • de choisir les bons axes, les bonnes échelles,

    • d’indiquer les noms des courbes et des axes,

    • de visualiser les tracés à l’écran

    • et de les sauvegarder dans des fichiers (pdf ou png).

  • En pratique, chaque action modifie l’état de la figure en cours d’élaboration.
    Une action est un appel de fonction plt.
    Il peut être utile de tracer plusieurs “sous-figures” au sein d’une même figure.

Le module python numpy est le compagnon naturel de matplotlib.

import numpy as np

13.2.2. matplotlib : comment ça le fait ?#

Une première prise en main grâce à :

De façon plus guidée :

Vocabulaire et notions de base

Le schéma suivant illustre les principales notions de base d’un tracé pyplot.

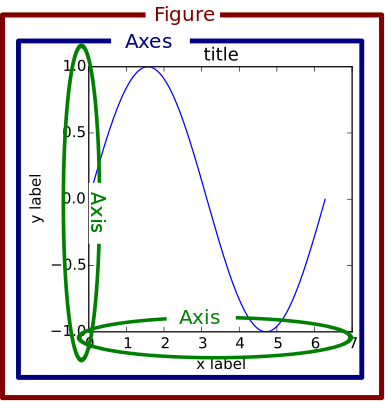
  • figure est un regroupement d’un ou plusieurs axes avec es (ie. un container python d’objets axes)

    • plusieurs axes sont stockés comme un tableau d’axes sous la forme d’un ndarray numpy (et donc avec un indiçage différent des list2D python)

  • un axes avec es (le pluriel de axis) représente un tracé (d’une ou plusieurs courbes, diagrammes en bâtons, …). Il est donc composé d’axis (avec is) : les “axes des x, des y”, d’échelles, de légendes, titres …

    • ne pas confondre axes et axis

    • axes est l’objet central : pour obtenir un tracé, on va manipuler un axes par des appels de fonctions-méthodes spécifiques

    • chaque appel modifie l’état de l’axes : définir des axis, leur échelle, tracer les courbes, ajouter un titre, … on procède par couches successives

      • le cas échéant on changera d’axes pour effectuer d’autres manipulations

    • et on affichera l’état final de la figure

Ces notions sont hiérarchiques :
figure > axes > (xaxis, yaxis, title, xlabel, …) > xticks,

On va montrer quelques commandes de base :

  • crée une figure et le/les axes (un par défaut) qui la compose : subplots()

  • afficher de courbes : plot, title, legend ;

  • gérer les axis : xticks, xlim, loglog, semilogx ;

  • gérer les affichages : show, savefig, close.

13.2.3. Exercice#

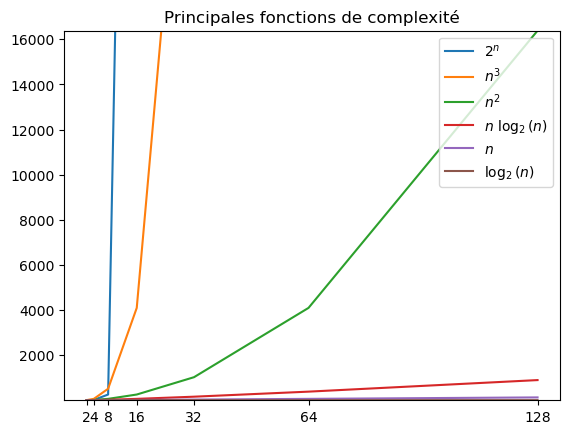
Obtenir le tracé des principales classes de complexités : \(log_2n\), \(n\), \(n\ \log_2(n)\), \(n^2\), \(n^3\), \(2^n\) pour les premières puissances de 2 – par exemple de 2 à 128.

A votre avis, pourquoi des échelles logarithmiques sont adaptées ?

Rmq.

  • La solution intègre en commentaires quelques commandes utiles au traitement hors des notebook, cad. dans un programme python écrit sous l’idle par exemple.

  • ligne 45 : elle suppose l’existence d’un répertoire ./tmp (à adapter si besoin)

Tip

Obtenir une figure pertinente est un vrai travail qui s’effectue en plusieurs itérations. Il est conseillé de “jouer” avec les différentes commandes jusqu’à obtenir le support graphique qui correspond au message que l’on veut faire passer, celui-ci devant être adapté au public visé.

# complexites.py
"""Trace des principales classes de complexites avec matplotlib"""

# la figure et ces zones de tracé : ici une seule (ax)
fig, ax = plt.subplots()

# son titre
ax.set_title("Principales fonctions de complexité")

# valeurs d'évaluations
n = [2**i for i in range(1,8)]  # les premieres puissances de 2  

# tracés des évaluations
ax.plot(n, np.power(2.0, n), label="$2^n$")
ax.plot(n, np.power(n, 3), label="$n^3$")
ax.plot(n, np.power(n, 2), label="$n^2$")
ax.plot(n, n*np.log2(n), label="$n\ \log_2(n)$")
ax.plot(n, n, label="$n$")
ax.plot(n, np.log2(n), label="$\log_2(n)$")

# ses axes en log2 : pour bien voir
#ax.set_xscale("log", base=2)
#ax.set_yscale("log", base=2)

# valeurs affichees sur l axe des x
label_x = [str(val) for val in n]
ax.set_xticks(n, label_x)

# valeurs affichees sur l axe des y
#y_val = [np.power(2, j) for j in range(0, 15, 2)]
#label_y = [str(val) for val in y_val]
#ax.set_yticks(y_val, label_y)

# on limite les valeurs de y trop grandes
ax.set_ylim(1.0, np.power(2,14))
#

# afficher la légende à cette position
ax.legend(loc="upper right")

# sortie ecran (inutile sous notebook)
#fig.show()

<matplotlib.legend.Legend at 0x1227c6690>
../_images/a8998c42ef8c27cd3f342bbb9f7be6c8644cc3573356f3882eb772b2b0bbec2f.png 
#ou fichier pdf : suppose l'existence d'un repertoire ./tmp
from matplotlib.backends.backend_pdf import PdfPages 

fig = plt.figure(figsize=(10,8), dpi = 80)  # size est en pouce...
pp = PdfPages('./tmp/plt-complexites.pdf')
pp.savefig()
pp.close()

<Figure size 800x640 with 0 Axes>

13.2.4. Manipuler des images avec matplotlib#

Il est classique de définir des images à niveaux de gris par un tableau 2D d’entiers compris en 0 (noir) et 255 (blanc) – voir par exemple la Feuille 3.

Voyons comment afficher de telles images avec matplotlib.

Si ce n’est pas encore fait, on importe matplotlib.pyplot

import matplotlib.pyplot as plt

On définit 4 images basiques à l’aide de tableaux python.

l = 3
c = 4

t0 = [[0 for i in range(c)] for j in range(l)] # un tableau de 0
t127 = [[127 for i in range(c)] for j in range(l)] # un tableau de 127
t255 = [[255 for i in range(c)] for j in range(l)] # # un tableau de 255

# un degradé de valeurs de 0 à 255
unit = int(255/(l*c)) 
t = [[ (i + j*c) * unit for i in range(c)] for j in range(l)] 

print(t)

[[0, 21, 42, 63], [84, 105, 126, 147], [168, 189, 210, 231]]

Avec la fonction-méthode .matshow(), on affiche les images correspondants aux tableaux définis plus haut.
On note les paramètres effectifs qui définissent comment interpréter les valeurs du tableau :

  • cmap (color map) ici une échelle de gris définie à partir de :

  • vmin jusqu’à

  • vmax.

fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(8, 4))

ax1.matshow(t0, cmap="gray", vmin=0, vmax=255)
ax2.matshow(t127, cmap="gray", vmin=0, vmax=255)
ax3.matshow(t255, cmap="gray", vmin=0, vmax=255)
ax4.matshow(t, cmap="gray_r", vmin=0, vmax=255)

#for ax in (ax1, ax2, ax3, ax4):
#    ax.tick_params(axis='both', which='both', **nolabels)

<matplotlib.image.AxesImage at 0x122fbb6d0>
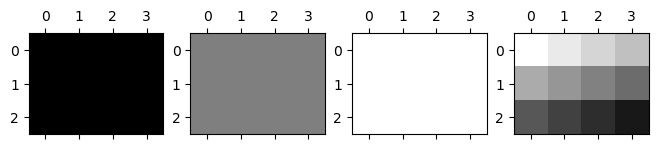
../_images/564c0f777db4edce5831dd122c874100c30342a95980992de2fc520203fa5333.png

On va nettoyer cet affichage à l’aide du dictionnaire nolabels et de

On supprime les indications d’axes adaptées aux courbes mais inutiles ici. La modification est sauvegardée dans un dictionnaire (nolabels) qui sera utilisé avant l’affichage. Oui ! En l’état de vos connaissances, ce traitement peut vous paraître un peu chimique …

sides = ('left', 'right', 'top', 'bottom')
nolabels = {s: False for s in sides}
nolabels.update({'label%s' % s: False for s in sides})
print(nolabels)

{'left': False, 'right': False, 'top': False, 'bottom': False, 'labelleft': False, 'labelright': False, 'labeltop': False, 'labelbottom': False}

fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(8, 4))

ax1.matshow(t0, cmap="gray", vmin=0, vmax=255)
ax2.matshow(t127, cmap="gray", vmin=0, vmax=255)
ax3.matshow(t255, cmap="gray", vmin=0, vmax=255)
ax4.matshow(t, cmap="gray_r", vmin=0, vmax=255)

for ax in (ax1, ax2, ax3, ax4):
    ax.tick_params(axis='both', which='both', **nolabels)
../_images/be2b6896673ad413b008a4cc705a65ae733bd91dc8eb8191f2c8ddf4015d436d.png

Voilà exactement ce qu’on souhaitait !

Exercice.

  • Regardez ce que donne la cmap="gray_r" ?

13.2.5. A vous maintenant !#

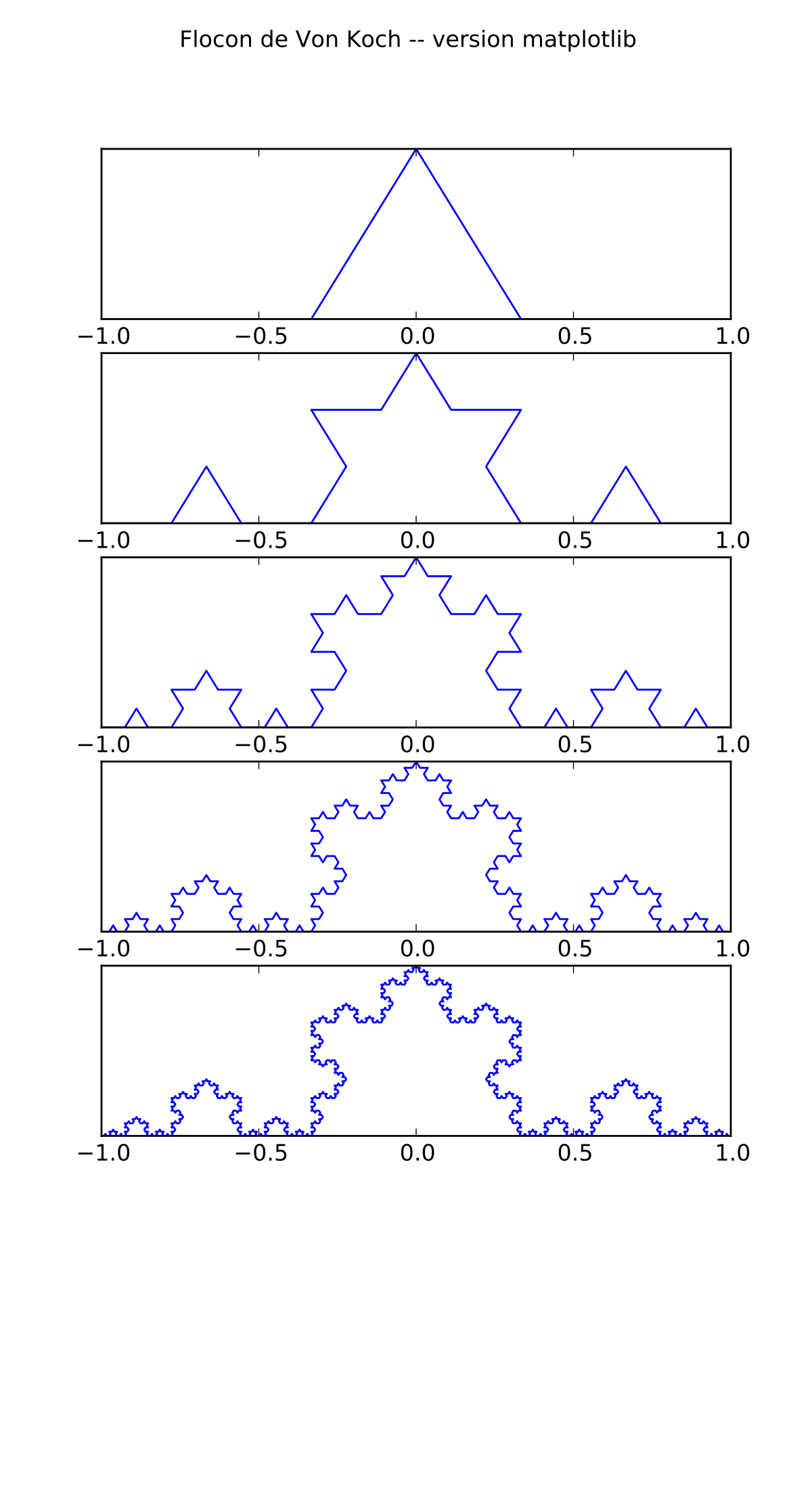
Le flocon de Von Koch#

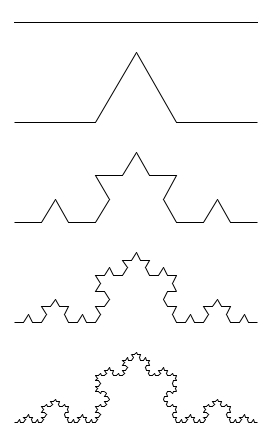
Le flocon de Von Koch (1906) est une courbe fractale (continue partout et dérivable nulle part) obtenue comme la limite de la transformation suivante appliquée récursivement à un segment de départ.

  • le segment est découpée en 3 parties égales,

  • le segment intermédiaire est remplacé par deux segments formant un triangle équilatéral avec le segment supprimé,

  • et ainsi de suite sur les 4 segments ainsi obtenus.

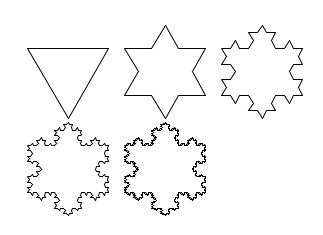
Voici les cinq premières courbes obtenues à partir d’un segment droit ou d’un triangle équilatéral : le flocon de Von Koch.
On parle aussi de courbe de Von Koch d’ordre \(n\) pour la courbe de la \(n\)-ième récursion – les tracés suivants correspondent aux segments de Von Koch d’ordres \(0, \cdots, 4\).

from IPython.display import Image 
Image(filename='./fig/cinqsegmentsvk.jpg')
../_images/a92acd5c167b9f1eb7f805e6e9c4cb35c99fa691f4f751d3b3e6a502ed596a46.jpg 
Image(filename='./fig/cinqflocons.jpg')
../_images/59fc5037f117c1f88c1ef9da7b13109c0bddb406a082f22e29bb814c97a67fb8.jpg

Traçons-le !

On va se limiter à celui avec un segment de départ.
Avec matplotlib, on choisit de calculer les coordonnées des sommets des transformés successifs du segment de départ, puis de les tracer comme une courbe.

  1. Écrire la fonction segvk() qui à partir des extrémités d’un segment \([a, b]\), par exemple définies par ses affixes complexes, calcule et retourne la liste (des affixes) des points significatifs d’une itération de Von Koch de \([a, b]\).

  2. Écrire la fonction listevk() qui applique une itération de Von Koch à une liste de segments.

  3. Apliquer ces fonctions pour obtenir le tracé matplotlib des premières itérations du segment \([-1, 1]\).

Il est agréable d’obtenir ces tracés sous la forme de sous-figures comme présenté ci-dessus.

Image(filename='./fig/plt-segvk.png', width=520 )
../_images/eb2c9fb60fd302293b70701a9e60e0d4422cdf1ae972628b10801d027c073332.png

13.3. (\(\star\)) Mesurer le temps d’exécution d’un programme#

13.3.1. Pas si simple …#

Mesurer le temps d’exécution d’un programme sur une machine actuelle est une une tâche beaucoup plus ardue qu’il n’y parait. En effet, l’impression que l’exécution de votre programme mobilise à elle seule les ressources de votre ordinateur est une illusion.

Le temps que vous attendez pour obtenir votre résultat, même si cela vous parait instantané, est en fait partagé : pendant ce même temps, votre ordinateur effectue certainement de nombreuses autres tâches, par exemple liées au système d’exploitation, aux périphériques, à d’autres utilisateurs si votre machine gère plusieurs sessions, …

Par ailleurs, les unités de calculs et l’organisation (des niveaux) de la mémoire compliquent très fortement la mesure fiable des temps d’exécution et leur analyse.

En pratique, plus ce que vous voulez mesurer est court, plus la mesure sera incertaine et non reproductible.

Pour ce qui nous intéresse, l’obtention d’une mesure significative consistera à :

  1. répéter l’exécution dans une boucle,

  2. mesurer le temps d’excution de cette boucle et

  3. en retenir la moyenne. Il n’est pas inutile de répéter ce type de mesures et le cas échéant de traiter l’échantillon obtenu.

Les “gros problèmes” sont aussi sujets à remarque.

  • Des tailles de données importantes nécessitent un volume important de transferts entre la mémoire et les unités de calcul.

  • Ces transferts mémoire sont complexes ;

  • leurs temps est :

    • d’une part non linéaire par rapport à la taille des données,

    • et d’autre part beaucoup plus important que les temps de calcul souvent associés.

A titre indicatif, il y a un facteur 10 entre ce temps de transfert et le temps d’un calcul arithmétique élémentaire.

  • ce qui veut dire qu’il faut 10 fois plus de temps pour lire deux valeurs en mémoire que pour faire leur addition, par exemple.

Ainsi, les mesures peuvent être surprenantes lorsqu’elles deviennent “dominées” par ces temps de transfert.
Le modèle de nos analyses de la complexité des algorithmes ne prend pas en compte cet aspect vite technique.

Pour finir, ceci illustre la différence entre les propriétés d’un algorithme et celles de ses mises en oeuvre et, par la même occasion, confirme l’intérêt des notations asymptotiques \(\cal{O}\), \(\theta\), \(\Omega\) dont on a souvent signalé qu’elle masquent pas mal de détails.

13.3.2. Mesurer avec le module time#

Ce module python fournit beaucoup de fonctions en rapport avec le temps : gestions de calendriers, des systèmes horaires, d’horloges …

Il permet aussi une estimation des temps d’exécution des programmes python (et autres). La qualité de cette estimation dépend des mises en oeuvre de ce module et des machines visées. Vous pouvez être relativement confiant sur vos PC-linux ou mac.

  • La fonction time() est annoncée avec une précision de la seconde, sans que ce soit garanti pour toutes les machines.
    Une seconde : c’est beaucoup ! C’est en effet suffisamment long pour effectuer 2 giga = 2 \(\cdot 10^9\) opérations …
    time() peut donc être utile pour des mesures grossières ou des exécutions de très gros volumes.

  • La fonction perf_counter() est définie depuis python3.3.
    Lorsqu’elle est disponible, elle permet les mesures les plus fines possibles adaptées à la mesure des temps d’exécution de programmes (sans être pour autant exacte, ni reproductible).
    Elle utilise des fonctions spécifiques aux architectures des machines qui exploitent les compteurs matériels.

Ces fonctions sont très simples à utiliser
On procède en deux appels qui encadrent la portion de code à mesurer.

  • t0 = time.perf_counter(): le premier appel initialise une valeur initiale t0;

  • t = time.perf_counter(): le second appel mesure t à l’issue de l’exécution de la portion de code

  • t - t0 est la mesure de ce temps d’exécution (moyennant les réserves précédentes).

Ne pas oublier de boucler autour de la portion à analyser et de mesurer à l’extérieur de cette boucle.

13.3.3. Un benchmark en \(\theta(n)\) : la somme itérative#

sommer() : l’algorithme classique par accumulation itérative.

def sommer(t, dim_t):
    '''somme itérative de n valeurs entières stockées dans un tableau
    entrées. t : tab d'int de longueur n
    retourne. res : int
    '''
    res = 0
    for i in range(dim_t):
        res = res + t[i]
    return res

# les 10 premiers entiers
tab10 = [i for i in range(1, 10)]

# somme itérative
s1 = sommer(tab10, len(tab10))

# somme des n premiers entiers
n = len(tab10)
s2 = n * (n+1) //2

print(s1, ' = ', s2)

45  =  45

13.3.4. Un premier exemple#

où on compare time.time() et time.perf_counter()

# pour afficher les sorties matplotlib dans le notebook
%matplotlib inline

import time
from random import *

# formats affichage : fx.format(val)
fint = "{:0=8}" #entier sur 7 digits complete avec 0 a gauche
fexp = "{:7.3e}"#float en notation e sur 7 digits dont 3 apres le .
ffl = "{:5.1f}" #float sur 5 digits dont au plus 1 apres le .

# timings operations en O(n) 
dim = 10000
dimmax = dim

# 1. avec des listes python
a = [random() for i in range(dimmax)]
b = [random() for i in range(dimmax)]

# nb repetititions de chaque mesure
nbrepet = 20

# time : timings operations en O(n) 
# les mesures sont à l'intérieur de la répétition
# car on veut évaluer la sensibilité de ces bestiolles

t_time = [] # les mesures
for repet in range(nbrepet): 
    # la mesure
    t0 = time.time()
    r = sommer(a, dimmax)
    t = time.time()
    #
    t_time.append(t-t0)

# perf_counter
t_tsc = [] # les mesures
for repet in range(nbrepet):
    # la mesure
    t0 = time.perf_counter()
    r = sommer(a, dimmax)
    t = time.perf_counter()
    #
    t_tsc.append(t-t0)

# aff mesures    
for r in range(nbrepet):
    print(fexp.format(t_time[r]) , fexp.format(t_tsc[r]))

1.640e-04 1.619e-04
1.621e-04 1.617e-04
1.669e-04 1.614e-04
1.650e-04 1.616e-04
1.659e-04 1.645e-04
1.662e-04 1.618e-04
1.690e-04 1.666e-04
1.678e-04 1.708e-04
1.621e-04 1.648e-04
1.609e-04 1.616e-04
1.609e-04 1.615e-04
1.607e-04 1.621e-04
1.612e-04 1.672e-04
1.609e-04 2.933e-04
1.612e-04 1.661e-04
1.609e-04 1.658e-04
1.612e-04 1.612e-04
1.647e-04 1.616e-04
1.621e-04 1.650e-04
1.640e-04 1.612e-04

### trace

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.set_yscale("log", base=10)
ax.plot(t_time, 'ro-', label="time")
ax.plot(t_tsc, 'b+-', label="perf_counter")
#
ax.legend(loc='upper right')
ax.set_title('20 mesures répétées')

#fig.show()
#plt.close()

Text(0.5, 1.0, '20 mesures répétées')
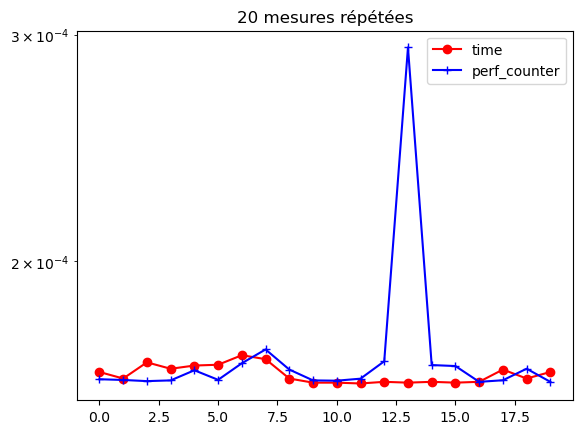
../_images/200e5964e06e5e35f97632b13a5e538764220d7fe9fd59e011cdaba41fb17d6d.png

13.4. Première mesure de complexité#

13.4.1. Des données de taille variable#

L’analyse de complexité dépend de la taille des entrées : \(n\).
Allons-y pour des mesures comme fonction de cette taille.

On fait ça avec time.time().

# timings operations en O(n) 

# 1. créer des données
dim = [10**i for i in range(2,8)]
dimmax = dim[len(dim)-1]
a = [random() for i in range(dimmax)]

### plus tard :  avec des ndarray et boucle sommer
# creation de ndarray numpy a partir de liste python (conversion)
#aa = np.array(a)

timings_array = []  # les mesures
ratio_array = []    # les ratios

# 2. mesurer
nbrepet = 10
for n in dim: # on parcours les différentes tailles
    t0 = time.time()
    for repet in range(nbrepet): # répéter les exécutions
            sommer(a, n)
    t = time.time()
    
    # timing moyen pour chaque dimension
    tmoy = (t-t0)/nbrepet
    timings_array.append(tmoy)
    ratio_array.append(tmoy/n)

# 3. aff de controle
for n in range(len(dim)):
    print(fint.format(dim[n]), fexp.format(timings_array[n]), fexp.format(ratio_array[n]))

# 4. tracer
fig, ax = plt.subplots()

ax.plot(dim, timings_array, 'ro-', label="sommer")
ax.plot(dim, ratio_array, 'go-', label="sommer / n ")

ax.set_xscale("log", base=10)
ax.set_yscale("log", base=10)

ax.set_xlabel("n : nombre de valeurs à sommer")
ax.set_ylabel("temps d'exécution (en sec) ou ratio temps/taille")
ax.legend(loc='upper left')

00000100 2.909e-06 2.909e-08
00001000 1.709e-05 1.709e-08
00010000 1.731e-04 1.731e-08
00100000 1.750e-03 1.750e-08
01000000 1.749e-02 1.749e-08
10000000 1.778e-01 1.778e-08

<matplotlib.legend.Legend at 0x12280ecd0>
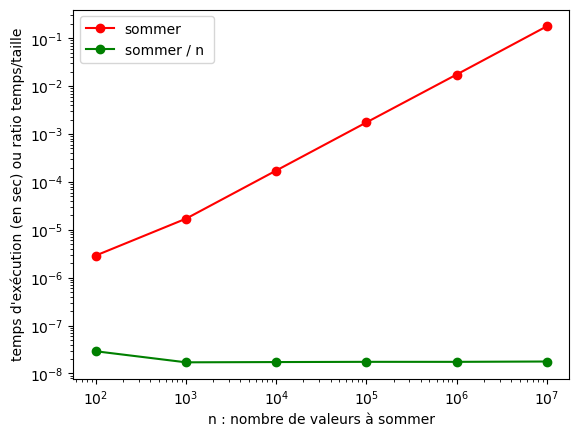
../_images/f97b87361d6dc639e9942e8b26b5bd82be7e73767f447cf51c9ad0598de008c7.png

Conclusion

  • on observe bien un comportement linéaire, ie. en \(\theta(n)\).

Contents